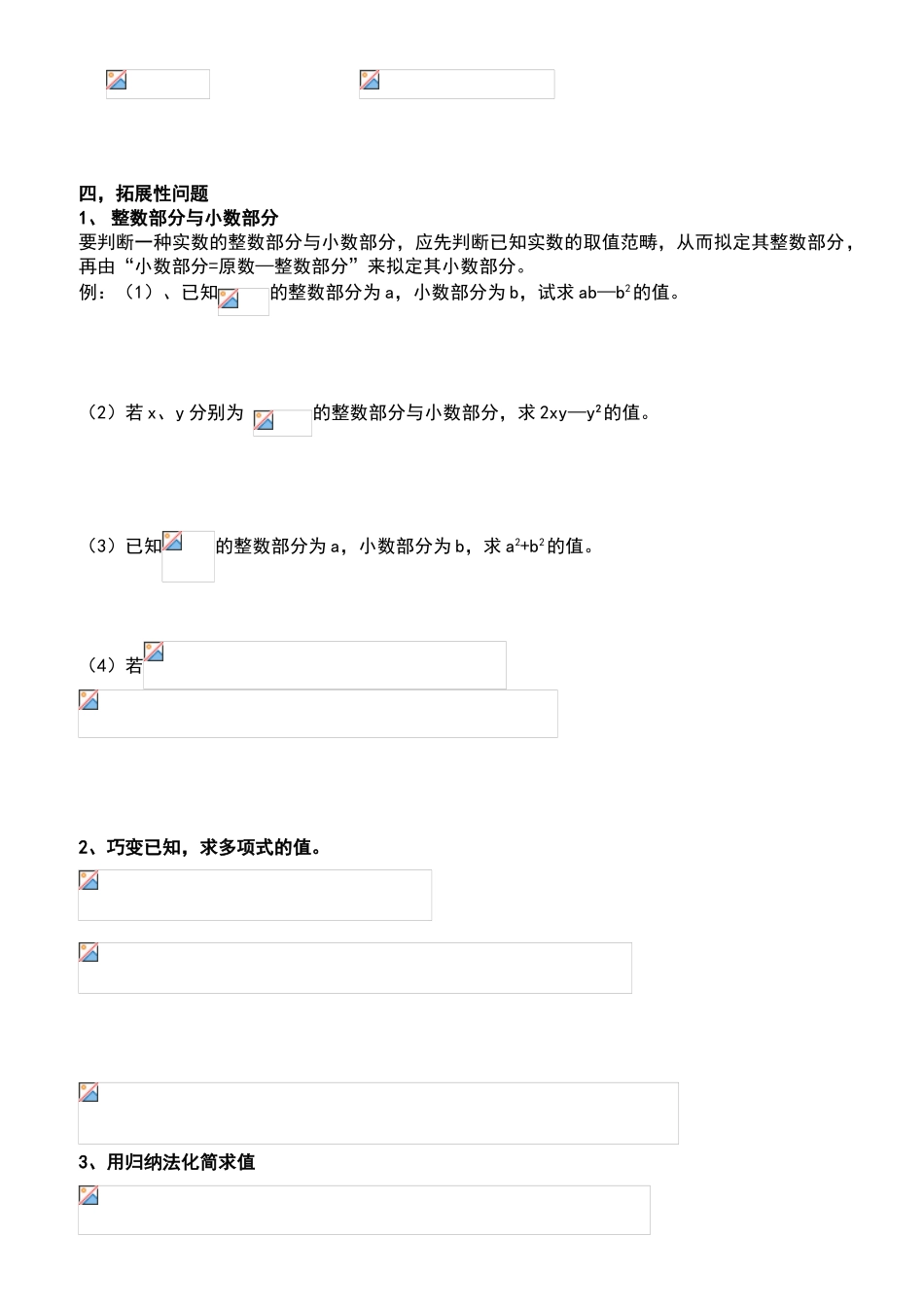
二次根式培优一、知识的拓广延伸1、挖掘二次根式中的隐含条件普通地,我们把形如的式子叫做二次根式,其中。根据二次根式的定义,我们懂得:被开方数a的取值范畴是,由此我们判断下列式子故意义的条件:2、的化简教科书中给出:普通地,根据算术平方根的意义可知:,在此我们可将其拓展为:(1)、根据二次根式的这个性质进行化简:①数轴上表达数a的点在原点的左边,化简=②化简求值:;其中a=③已知,,化简④;⑤若为a,b,c三角形的三边,则;⑥计算:.(2)、根据二次根式的定义和性质求字母的值或取值范畴。①若,求m的取值范畴。②若,则x的取值范畴是___________.③若,求的值;④二.二次根式二.二次根式的双重非负性质:的双重非负性质:①被开方数是非负数,即②二次根式是非负数,即例例1.1.要使故意义,则x应满足().A.≤x≤3B.x≤3且x≠C.<x<3D.<x≤3例例22((11))化简=_______.(2)若=(x+y)2,则x-y的值为()(A)-1.(B)1.(C)2.(D)3.例例33(1)若a、b为实数,且满足│a-2│+=0,则b-a的值为()A.2B.0C.-2D.以上都不是(2)已知是实数,且与互为相反数,求实数的倒数。三,如何把根号外的式子移入根号内我们在化简某些二次根式时,有时会用到将根号外的式子移入根号内的知识,这样式子的化简更为简朴。在此我们要特别注意先根据二次根式的意义来判断根号外的式子的符号。如果根号外的式子为非负值,可将其平方后移入根号内,与原被开方数相乘作为新的被开方数,根号前的符号不会发生变化;如果根号外的式子为负值,那么要先将根号前的符号变号,再将其其平方后移入根号内,与原被开方数相乘作为新的被开方数。(1)、根据上述法则,我们试着将下列各式根号外的式子移入根号内:①,②(2)、运用此办法可比较两个无理数的大小。四,拓展性问题1、整数部分与小数部分要判断一种实数的整数部分与小数部分,应先判断已知实数的取值范畴,从而拟定其整数部分,再由“小数部分=原数—整数部分”来拟定其小数部分。例:(1)、已知的整数部分为a,小数部分为b,试求ab—b2的值。(2)若x、y分别为的整数部分与小数部分,求2xy—y2的值。(3)已知的整数部分为a,小数部分为b,求a2+b2的值。(4)若2、巧变已知,求多项式的值。3、用归纳法化简求值五.其它五.其它例例11.11.观察分析下列数据,寻找规律:0,,……那么第10个数据应是。例例12.12.(1)已知n是一种正整数,是整数,则n的最小值是()。A.3B.5C.15D.25(2).已知是正整数,则实数n的最大值为()A.12B.11C.8D.326.有这样一类题目:将化简,如果你能找到两个数m、n,使并且,则将变成开方,从而使得化简。例如:化简仿照上例化简下列各式:(6分)(1)(2)(二)勾股定理提高题一、选择题1、直角三角形的斜边比始终角边长2cm,另始终角边长为6cm,则它的斜边长()A、4cmB、8cmC、10cmD、12cm2、如图①小方格都是边长为1的正方形,则四边形ABCD的面积是()A、25B、12.5C、9D、8.53、△ABC是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°,AC=30米,AB=50米,如果要在这块空地上种植草皮,按每平方米草皮元计算,那么共需要资金().A、50元B、600元C、1200元D、1500元4、如图②是一株美丽的勾股树,其中全部的四边形都是正方形,全部的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是()A、13B、26C、47D、945、已知一种Rt△的两边长分别为3和4,则第三边长的平方是()A、25B、14C、7D、7或256、等腰三角形的腰长为10,底长为12,则其底边上的高为()A、13B、8C、25D、647、已知x、y为正数,且│x2-4│+(y2-3)2=0,如果以x、y的长为直角边作一种直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为()A、5B、25C、7D、158、△ABC中,若AB=15,AC=13,高AD=12,则△ABC的周长是()A.42B.32C.42或32D.37或339、如图③,长方体的长为15,宽为10,高为20,点B离点C的距离为5,上只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A、5B、25C、+5D、3510、如图④,AB⊥CD于B,△ABD和△BCE都是等腰...