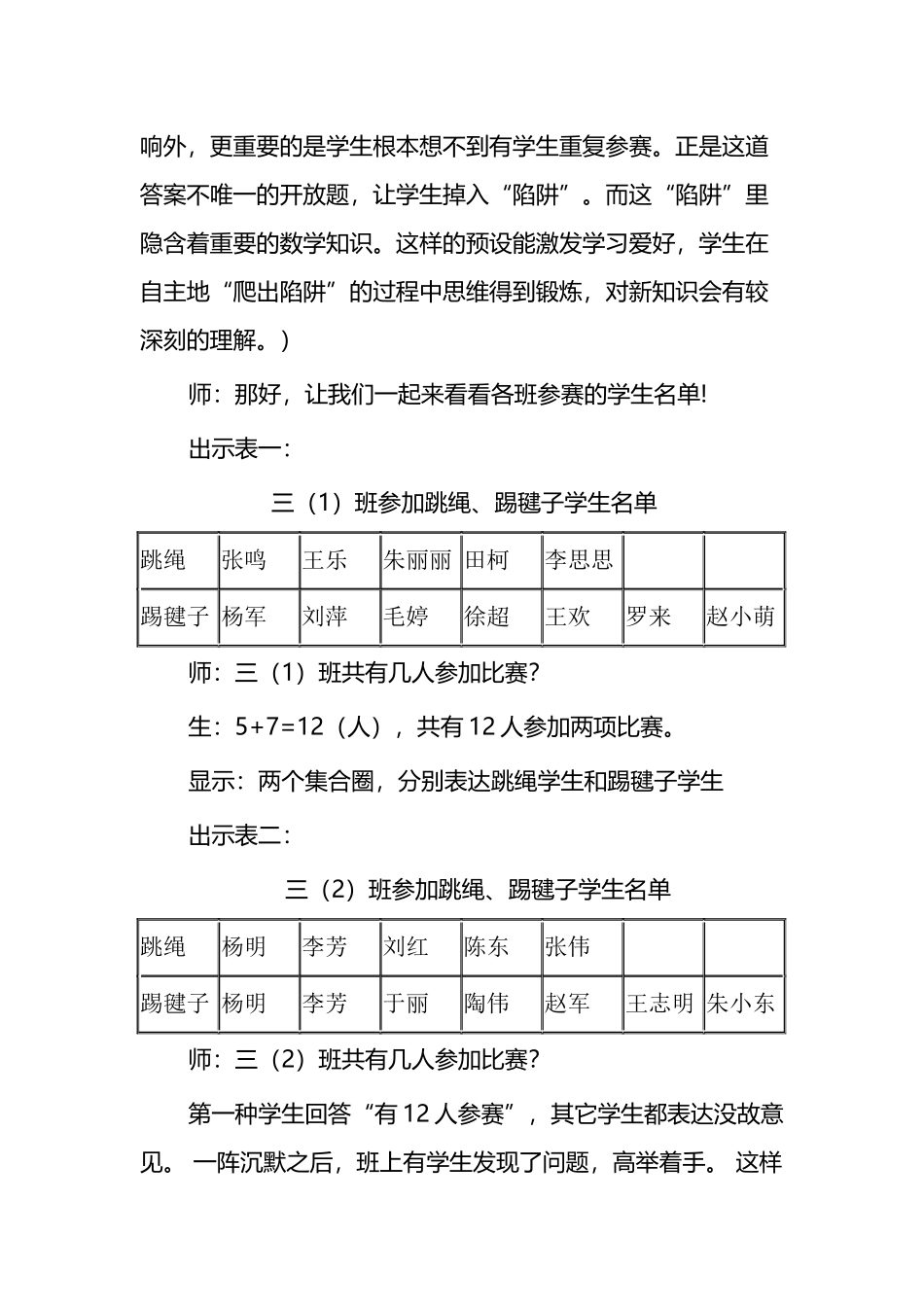
重叠问题”教学设计教学目的:1、让学生经历探究用集合图表达两个集合关系的活动过程,理解集合图所示的含义,学习用集合的思想办法来思考和解决实际问题。2、让学生感受到数学与生活的亲密联系,体验数学的价值。教学过程:一、引入。出示:小朋友们在食堂排成一队打饭,亮亮从前面数是第5个,从背面数还是第5个,这个队一共有多少个同窗?(学生出现不同的答案:11个、12个、9个)师:怎么有不同的答案?怎么办?(生:计算、画图。)教师找计算和画图的两位学生到黑板上板演,其它学生自己在练习本上解决。生:○○○○△○○○○师:真聪颖!他还把亮亮用不同的图形来表达。一块数一数多少人。(生快数)师:在图上找一找,从前面数的5在哪儿?圈一圈。从背面数的5在哪儿?也圈一圈。师:你发现了什么?生:亮亮被数了两次。师:因此要用10-1=9,看来确实是9个人。想一想,是谁帮我们弄明白的?生:圈二、展开。出示:“实验小学三年级定于下周二下午举办跳绳比赛,下周五下午举办踢毽子比赛。三年级共有3个班级,每班选7个学生参加跳绳比赛,选5个学生参加踢毽子比赛。三年级共有多少名学生参加了跳绳、踢毽子比赛?”学生默读题目,独立思考,列式计算。全班交流:办法一:3×7+3×5=36(人)办法二:(7+5)×3=36(人)追问:有不同意见吗?必定共有36人吗?学生一致表达必定。(分析:学生之因此敢这样必定,由于他们习惯于解答“条件个个有用、答案唯一”这类问题。除了习惯性思维的影响外,更重要的是学生根本想不到有学生重复参赛。正是这道答案不唯一的开放题,让学生掉入“陷阱”。而这“陷阱”里隐含着重要的数学知识。这样的预设能激发学习爱好,学生在自主地“爬出陷阱”的过程中思维得到锻炼,对新知识会有较深刻的理解。)师:那好,让我们一起来看看各班参赛的学生名单!出示表一:三(1)班参加跳绳、踢毽子学生名单跳绳张鸣王乐朱丽丽田柯李思思踢毽子杨军刘萍毛婷徐超王欢罗来赵小萌师:三(1)班共有几人参加比赛?生:5+7=12(人),共有12人参加两项比赛。显示:两个集合圈,分别表达跳绳学生和踢毽子学生出示表二:三(2)班参加跳绳、踢毽子学生名单跳绳杨明李芳刘红陈东张伟踢毽子杨明李芳于丽陶伟赵军王志明朱小东师:三(2)班共有几人参加比赛?第一种学生回答“有12人参赛”,其它学生都表达没故意见。一阵沉默之后,班上有学生发现了问题,高举着手。这样一来,其它学生认真地看着屏幕。渐渐地,举手的学生越来越多,有的学生情不自禁地说:我故意见!师:刚刚大家都没故意见,现在怎么又故意见了呢?终于,有学生不好意思地说:刚刚我没看清晰,三(2)班的杨明和李芳,两项比赛都参加了,因此共有10人参加跳绳、踢毽子比赛。追问:若要让人清晰地看出跳绳的、踢毽的、既跳绳又踢毽的各有哪些人,用圈如何表达?让学生尝试画圈。(分析:学生很快回答“三(2)班有10人参赛,可能是由三(1)班的状况作出想固然的回答(没有认真看名单),但也可能确实没有看清晰。于是,“若要让人清晰地看出参加跳绳的、参加踢毽的、既参加跳绳又参加踢毽的,用圈如何表达?”成为学生本身想要解决的问题,并且是一种没有现成办法能够解决的问题。可见,教师预设问题时,要考虑学生学习中的障碍、困惑,真正使“问题”成为“属于学生自己的问题”。这样的问题才是真问题;只有真问题,才干激发学生的学习需求,才干让学生主动主动地投入解决问题的活动中去。)学生各自独立思考着、尝试着用圈表达,出现了多个不同的想法,思维激烈地碰撞了起来——生1:我是画了两个圈,在重复参赛的学生名字的下面画上小圆点,这样让别人能清晰地看出重复参赛的学生。师:你们同意吗?生:我认为有点看不太清晰,由于找小圆点也会很费力的。生2:我是用三个圈来表达的,你们能看懂吗?生3:杨明、李芳都参加了两项比赛,可是,为什么在跳绳和踢毽的圈里没有他们呢?我是这样画的(上黑板前画出图),中间的是既跳绳又踢毽的学生。师:大家尚有别的意见吗?生4:即使能看清晰两样比赛都参加的学生,但是,我不懂得哪个圈里是跳绳的,哪个圈里是踢毽子的。生3又在圈上面标上了“跳绳”、“踢...