高一数学(正弦函数、余弦函数的图象)课件VIP免费

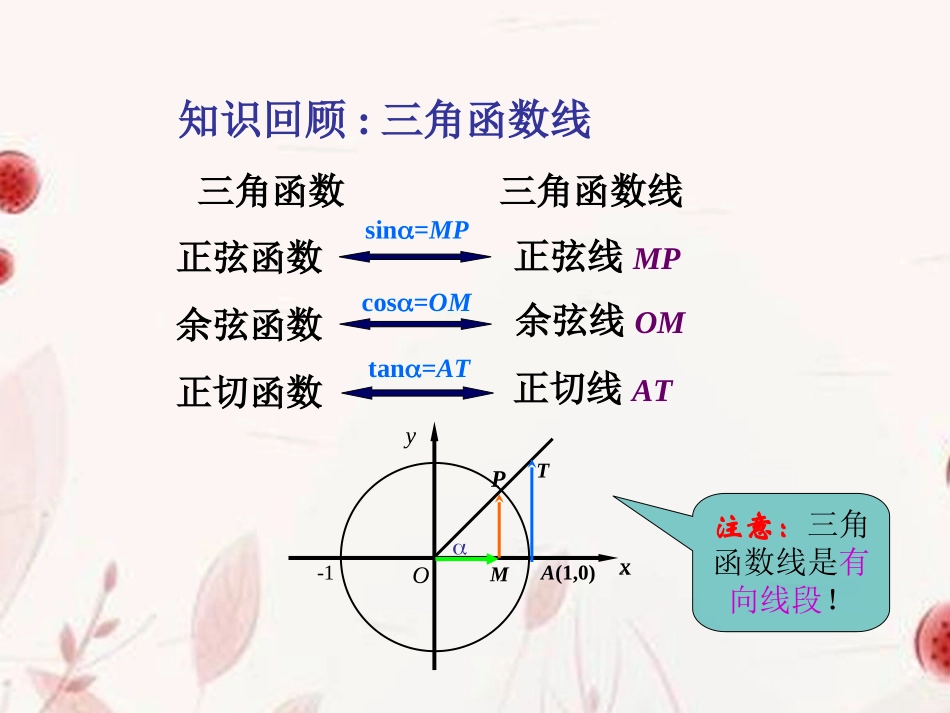
1.4.1正弦函数、余弦函数的图象观察与发现：简谐振动图象你能从中发现什么？三角函数三角函数线正弦函数余弦函数正切函数正切线AT知识回顾:三角函数线yxxO-1PMA(1,0)Tsin=MPcos=OMtan=AT注意：三角函数线是有向线段！正弦线MP余弦线OMPMC(,)33sinyxO1-13sin3在直角坐标系中如何作点（，）？、热身3正弦函数的图象问题：如何利用学过的知识作出正弦函数图象？途径：利用单位圆中正弦线来解决。O1Oyx33234352-11AB]2,0[,sinxxy66567236112正弦函数的图象y=sinxx[0,2]y=sinxxR终边相同角的三角函数值相等即：sin(x+2k)=sinx,kZ沿着x轴向右和向左连续地平行移动Rxxy,sinx6yo--12345-2-3-41每次移动的距离为2π正弦曲线x6yo--12345-2-3-41正弦、余弦函数的图象余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线正弦曲线形状完全一样只是位置不同观察与思考：观察我们用单位圆中的正弦线作出的函数ｙ＝sinｘ，ｘ∈〔0，２π〕的图象，你发现有哪几个点在确定图象的形状起着关键作用？yxo1-122322(0,0)(,1)2(,0)(,-1)23(2,0)五点画图法五点法——(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)yxo1-122322y=cosx，x[0,2]找出余弦函数y=cosx，x[0,2]图象五个关键点：方法总结：在精确度要求不高时，先作出函数ｙ＝sinｘ和y=cosx的五个关键点，再用平滑的曲线将它们顺次连结起来，就得到函数的简图。这种作图法叫做“五点（画图）法”。例1（1）画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-1012101o1yx22322-12y=1+sinx，x[0,2]步骤：1.列表2.描点3.连线典型范例：例1（2）画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=cosx，x[0,2]典型范例：合作探究例1（1）：o1yx22322-12y=1+sinx，x[0,2]y=sinx，x[0,2]总结：函数值加减，图像上下移动如何利用y=sinx，ｘ∈〔0，２π〕的图象，得到y＝1＋sinx,ｘ∈〔0，２π〕的图象？总结：这两个图像关于X轴对称。如何利用y=cosx，ｘ∈〔0，２π〕的图象，得到y＝-cosx，ｘ∈〔0，２π〕的图象？合作探究例1（2）：yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]xsinx2230210-101在同一坐标系内，用五点法分别画出函数y=sinx，x[0,2]和y=cosx，x[,]的简图，并说出它们之间的关系。o1yx22322-12y=sinx，x[0,2]y=cosx，x[,]223向左平移个单位长度2xcosx100-1022302练习1解：223π不用作图，你能判断函数和y=cosx的图象有何关系吗？)23sin(xy练习2xxxxycos)2sin(]2)23sin[()23sin(解：∵∴这两个函数图象相同正弦、余弦函数的图象正弦、余弦函数的图象小结1.正弦曲线、余弦曲线几何画法五点法2.注意与诱导公式、三角函数线等知识的联系yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]课后作业：①课本P46习题1.4A组1.