高三数学 8.9直线与圆锥曲线的位置关系复习课件VIP免费

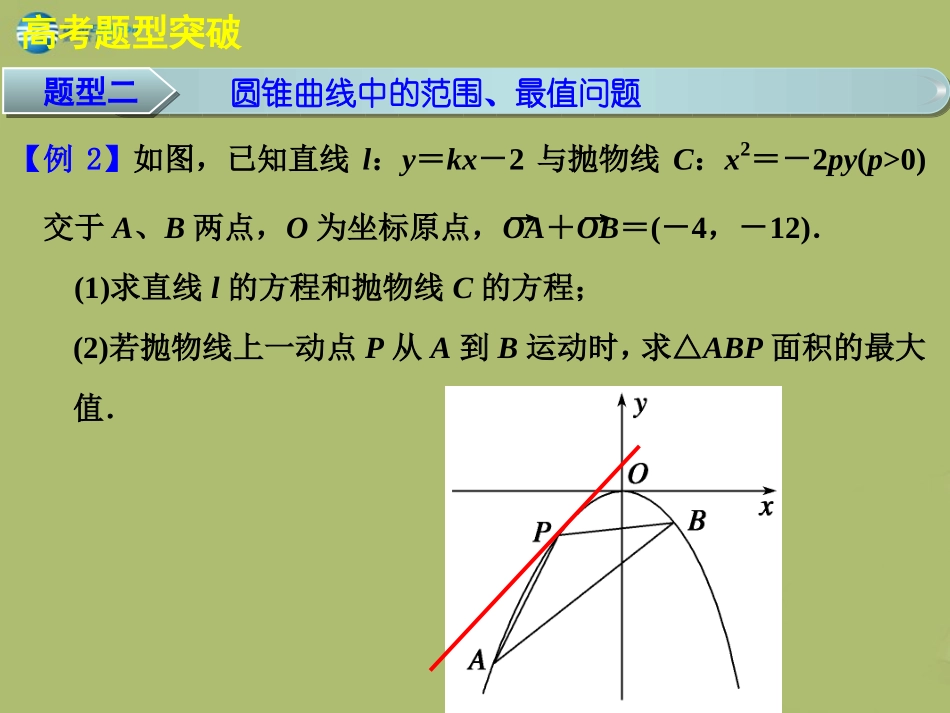
数学RB（理）第九章平面解析几何高考中的圆锥曲线问题高考中的圆锥曲线问题题型一求参数的取值范围跟踪训练1：如图所示，已知圆,8)1(:22yxC定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足0,2AMNPAPAM，点N的轨迹为曲线E.（1）求曲线E的方程；（2）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），且满足求,FHFG的取值范围.高考题型突破FGH题型二圆锥曲线中的范围、最值问题【例2】如图，已知直线l：y＝kx－2与抛物线C：x2＝－2py(p>0)交于A、B两点，O为坐标原点，OA→＋OB→＝(－4，－12)．(1)求直线l的方程和抛物线C的方程；(2)若抛物线上一动点P从A到B运动时，求△ABP面积的最大值．高考题型突破题型三圆锥曲线中的定点、定值问题【例3】(2012·福建)如图，等边三角形OAB的边长为83，且其三个顶点均在抛物线E：x2＝2py(p>0)上．(1)求抛物线E的方程；(2)设动直线l与抛物线E相切于点P，与直线y＝－1相交于点Q，证明：以PQ为直径的圆恒过y轴上某定点．高考题型突破既然圆过y轴上的点，即满足MP→·MQ→＝0，对任意P、Q恒成立可待定M(0，y1)，也可给定特殊的P点，猜想M点坐标，再证明．高考题型突破思维启迪思维升华解析题型二圆锥曲线中的定点、定值问题题型三圆锥曲线中的定点、定值问题【例3】(2012·福建)如图，等边三角形OAB的边长为83，且其三个顶点均在抛物线E：x2＝2py(p>0)上．(1)求抛物线E的方程；(2)设动直线l与抛物线E相切于点P，与直线y＝－1相交于点Q，证明：以PQ为直径的圆恒过y轴上某定点．高考题型突破PQM求定点及定值问题常见的方法有两种：高考题型突破(1)从特殊入手，求出定值，再证明这个值与变量无关．(2)直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．题型二圆锥曲线中的定点、定值问题题型三圆锥曲线中的探索性问题【例4】.已知中心在原点的椭圆C：x2a2＋y2b2＝1的一个焦点为F1(0,3)，M(x,4)(x>0)为椭圆C上一点，△MOF1的面积为32.(1)求椭圆C的方程；(2)是否存在平行于OM的直线l，使得直线l与椭圆C相交于A，B两点，且以线段AB为直径的圆恰好经过原点？若存在，求出直线l的方程；若不存在，说明理由．高考题型突破OFM(1)存在性问题通常采用“肯定顺推法”，将不确定性问题明朗化．其步骤为假设满足条件的元素(点、直线、曲线或参数)存在，用待定系数法设出，列出关于待定系数的方程组，若方程组有实数解，则元素(点、直线、曲线或参数)存在；否则，元素(点、直线、曲线或参数)不存在．高考题型突破思维升华(2)反证法与验证法也是求解存在性问题常用的方法．跟踪训练3已知椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点O，从每条曲线上各取两个点，将其坐标记录于下表中：(1)求C1，C2的标准方程；(2)是否存在直线l满足条件：①过C2的焦点F；②与C1交于不同的两点M，N，且满足OM→⊥ON→？若存在，求出直线l的方程；若不存在，说明理由．高考题型突破x3－242y－230－422OMONOMON�？高考题型突破解(1)设抛物线C2：y2＝2px(p≠0)，则有y2x＝2p(x≠0)，据此验证四个点知(3，－23)，(4，－4)在C2上，易求得C2的标准方程为y2＝4x.设椭圆C1：x2a2＋y2b2＝1(a>b>0)，把点(－2,0)，(2，22)代入得4a2＝12a2＋12b2＝1，解得a2＝4b2＝1，所以C1的标准方程为x24＋y2＝1.(2)容易验证当直线l的斜率不存在时，不满足题意．高考题型突破当直线l的斜率存在时，设其方程为y＝k(x－1)，与C1的交点为M(x1，y1)，N(x2，y2)．由x24＋y2＝1，y＝kx－1消去y并整理得(1＋4k2)x2－8k2x＋4(k2－1)＝0，于是x1＋x2＝8k21＋4k2，①x1x2＝4k2－11＋4k2.②所以y1y2＝k2(x1－1)(x2－1)＝k2[x1x2－(x1＋x2)＋1]＝k2[4k2－11＋4k2－8k21＋4k2＋1]＝－3k21＋4k2.③高考题型突破由OM→⊥ON→，即OM→·ON→＝0，得x1x2＋y1y2＝0.(*)将②③代入(*)式，得4k2－11＋4k2－3k21＋4k2＝k2－41＋4k2＝0，解得k＝±2，所以存在直线l满足条件，且直线l的方程为2x－y－2＝0或2x＋y－2＝0.题型五直线、圆及圆锥曲线的交汇问题【例4】(2013·浙江)如图，点P(0，－1)...