高中数学(幂函数)课件3 苏教版必修1 课件VIP免费

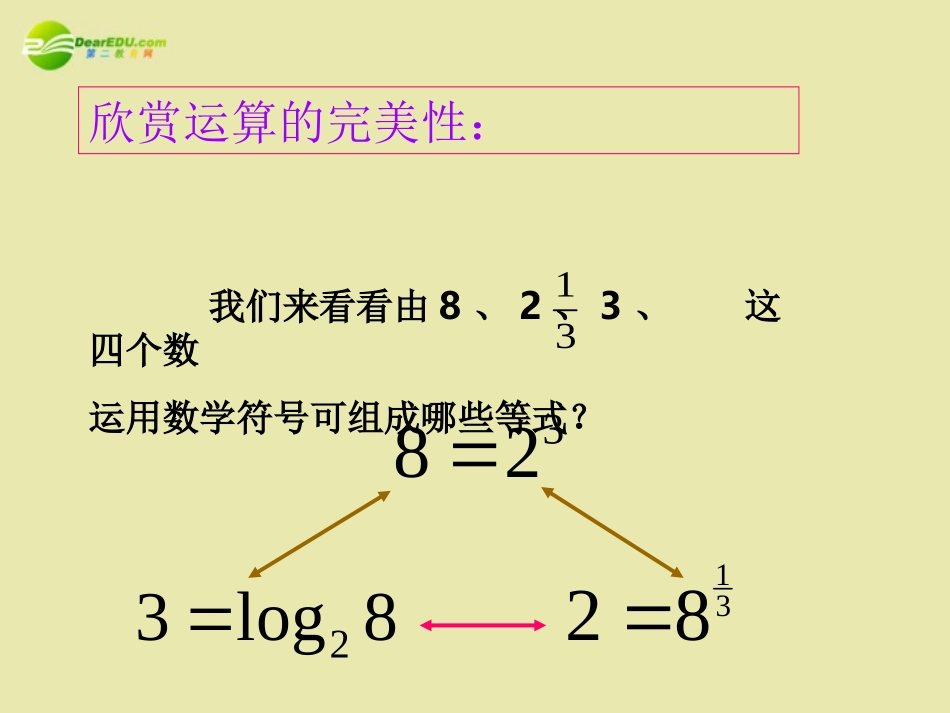
《幂函数》欣赏运算的完美性：32831828log32我们来看看由8、2、3、这四个数运用数学符号可组成哪些等式？31;1.xaybNa我们建立了指数函数的变化而变化，随一定，如果我们知道：Nab函数的完美追求。我们建立了对数函数：的变化而变化，随一定，如果xyNbaalog.2设想：bNa如果一定，随的变化而变化，是不是也应该可以确定一个函数呢？函数的生活实例问题1：如果张红购买了每千克1元的蔬菜w千克，那么她需要付的钱数p=元，。问题2：如果正方形的边长为a，那么正方形的面积是S=，。问题3：如果正方体的边长为a，那么正方体的体积是V=，。问题4:如果正方形场地的面积为S，那么正方形的边长a=，。问题5：如果某人ts内骑车行进了1km，那么他骑车的平均速度v=，。w这里p是w的函数a²这里S是a的函数a³这里V是a的函数21S这里a是S的函数这里v是t的函数1tkm/s我们把形如：的函数称为幂函数，其中是实常数。xy一幂函数的定义：------为了研究方便，我们只对是有理数的情况进行一些讨论5323)2()1(21xyxyxy）（研究几个具体的幂函数例1求下列函数的定义域，判断它们的奇偶性：例２判定函数y=x0.5在定义域上的单调性.重点研究幂函数在第一象限的图象因为函数的奇偶性能够帮助我们完成左半平面内的图象，所以只需要研究它们在第一象限内的图象1232,321213121xyxyxyxyxyxyxy和）（和）（和）（二幂函数在第一象限的图象利用Excel作出下列幂函数在第一象限的图象012301232xy3xy观察（一）0123012321xy31xy观察（二）21xy2xy1xy01230123观察（三）观察后归纳（四）通过计算机快速作图，我们观察到更多的幂函数图象。请注意幂函数的指数变化，带来的幂函数图象在第一象限的变化规律小组讨论，归纳——通过对图象位置变化的观察，我们可以发现哪些规律性的结论？填在课本第78页的表格内!精彩性质（五）把图象的变化“记录”下来y=xy=x2y=x3y=xy=x-1定义域RRR[0,+∞){x|x≠0}值域R[0,+∞)R[0,+∞){y|y≠0}奇偶性奇偶奇非奇非偶奇单调性增增增增减公共点(1,1)(1,1)(1,1)(1,1)(1,1)21归纳幂函数图象在第一象限的分布情况：10101001在上任取一点作轴的垂线，与幂函数的图象交点越高，的值就越大。),1(x.)0[)11()00(0上单调递增，在区间；，和，图象都过定点，归纳.)0()11(,0上单调递减，在区间；，图象都过定点幂函数图象在第一象限的性质：21,2,21,2)(21,2,2,21)(2,21,21,2)(2,21,21,2)(,,,2124321DCBAccccxy依次为的，则，已知在第一象限的图象，如图是幂函数0120121c2c3c4c知识理解、运用xy图象性质应用（奇偶性和单调性）1.画出幂函数的图象，并指出它的单调性2.比较下列各组数的大小.(1)(2)31xy11331.5,1.7,1333777(2),(3),(5)例3、试解下列各题课堂探究（1）若(a+1)-2>(3-2a)-2，求实数a的取值范围。（2）已知幂函数y=xm2-2m-3（m∈N)的图像与x轴、y轴都没有公共点，且关于y轴对称，求m的值。小结：1.学习了幂函数的概念；2.利用“还原根式”求幂函数定义域的方法；3.利用幂函数在第一象限内的图象特征，并会根据奇偶性完成整个函数的图象。4.利用函数的单调性比较几个“同指数不同底数”的幂的大小.关系？义域以及奇偶性有什么的定互质且的奇偶性与幂函数整数),,,(,nmZnmxynmnm课后再探究高考数学一轮复习课件——《幂函数》考试说明通过概念和图象了解幂函数通过概念和图象了解幂函数①通过实例，了解幂函数的概念.②结合函数，，，，的图象.了解它们的变化情况y=x1y=x2y=x3y=x12y=x1.幂函数的定义一般地，形如的函数称为幂函数，其中为常数.例如：知识要点()Ryxy=x1y=x2y=x3y=x12y=x知识要点2.形如的幂函数的奇偶性（1）当m，n都为奇数时，f（x）为奇函数，图象关于原点对称；（2）当m为奇数n为偶数时，f（x）为偶函数，图象关于y轴对称；（3）当m为偶数n为奇数时，f（x）是非奇非偶函数，图象只在第一象限内.()=(,)nnmN+fxxmZ其中知识要点3.幂函数的图象先画第一象限，然后根据奇偶性和定义域...