高中数学(抛物线的几何性质)课件 新人教版选修2-1 课件VIP免费

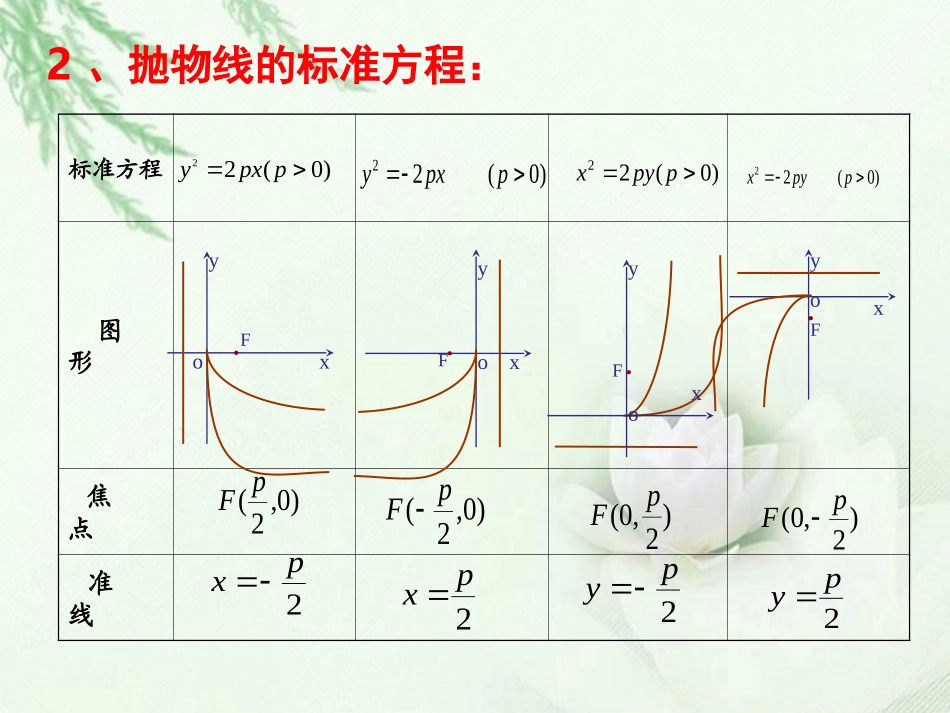
抛物线的简单几何性质（一）一、复习回顾：l定点F是抛物线的焦点，定直线叫做抛物线的准线.l.FMd.xOyK1、抛物线的定义：在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.标准方程图形焦点准线)0(22ppxy)0(22ppyx.xyFo)0,2(pF.yxoF2px)2,0(pF.xoyF2py)0(22ppxyxyoF.)0,2(pF2px)0(22ppyx)2,0(pF2py2、抛物线的标准方程：(1)范围(2)对称性(3)顶点x≥0,yR∈关于x轴对称,对称轴又叫抛物线的轴.抛物线和它的轴的交点(0,0)二、讲授新课：抛物线上的点到焦点的距离和它到准线的距离的比,叫做抛物线的离心率，用e表示，(4)离心率由抛物线的定义可知，e=1抛物线y2=2px(p>0)的几何性质:l.FMd.xOyK方程图形范围对称轴顶点离心率y2=2px（p＞0）y2=-2px（p＞0）x2=2py（p＞0）x2=-2py（p＞0）lFyxOlFyxOlFyxOx≥0yR∈x≤0yR∈xR∈y≥0y≤0xR∈lFyxO关于x轴对称关于x轴对称关于y轴对称关于y轴对称（0,0）1（0,0）（0,0）（0,0）111特点1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的,为1;基本点：顶点，焦点基本点：顶点，焦点基本线：准线，对称轴基本线：准线，对称轴基本量：焦准距基本量：焦准距pp（决定（决定抛物线开口大小）抛物线开口大小）三、例题解析：例2.边长为4的正三角形的一个顶点位于坐标原点，另外两个顶点在抛物线上，求抛物线方程三、典例精析)0(22ppxyyxO．M)2,32(解：设另一顶点为M,由题意知M坐标为)2,32(p32222xyp332332三、例题解析：例3.已知抛物线,设点A的坐标为，求抛物线上距离点A最近的点P的坐标及相应的距离.三、典例精析xy22)0,32(解：设抛物线上任一点P的坐标为(x,y))0,0(32031)31(2)32()32(min22222PPAxxxxyxPA此时则例4.斜率为1的直线l经过抛物线24yx的焦点F,且与抛物线相交于A,B两点,求线段AB的长.解这题,你有什么方法呢?12345678-1-2123456xyOABF1lyx直线的方程为：2216104yxxxyx解法1抛物线的焦点F(1,0),1212322322222222xxyy或221212AB=(x-x)+(y-y)=8例4.斜率为1的直线l经过抛物线24yx的焦点F,且与抛物线相交于A,B两点,求线段AB的长.1lyx的方程为：2216104yxxxyx22[]=116418AB22121214kxxxx解法2抛物线的焦点F(1,0),1212⇒x+x=6,xx=1例4.斜率为1的直线l经过抛物线24yx的焦点F,且与抛物线相交于A,B两点,求线段AB的长.1lyx的方程为：2216104yxxxyx解法3:抛物线的焦点F(1,0),1212⇒x+x=6,xx=1|AB|=|AF|+|BF|=|AA1|+|BB1|=(x1+1)+(x2+1)=x1+x2+2=812345678-1-2123456xyOABFA1B1例4.斜率为1的直线l经过抛物线24yx的焦点F,且与抛物线相交于A,B两点,求线段AB的长.（二）焦点弦：通过焦点的直线，与抛物线相交于两点，连接两点的线段叫做抛物线的焦点弦。12ABxxpxOyFA),(11yxB),(22yx特别的，过焦点而垂直于对称轴的弦AB，称为抛物线的通径。|AB|=2p焦点弦公式：利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.（一）焦半径：连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。焦半径公式：12pAFx变式:抛物线x2=4y的焦点为F,斜率为2的直线经过抛物线的焦点,且与抛物线相交于A,B两点,求线段AB的长.xoy.F解:抛物线的焦点F(0,1),21lyx的方程为：222118104yxyyxyyy1212+y=18,y=1|AB|=|AF|+|BF|=|AA1|+|BB1|=(y1+1)+(y2+1)=y1+y2+2=20AA1BB112345-1-1-2-3-4-512345xyO拓展提高：抛物线y2=4x的焦点为F,点M在抛物线上运动,A(2,2),试求|MA|+|MF|的最小值.MFAA1M1解|MA|+|MF|=|MA|+|MM1|≥|AA1|=3即|MA|+|MF|的最小值为3.（一）本节课我们学习了抛物线的几个简单几何性质：范围、对称性、顶点坐标、离心率等概念及其几何意义。（二）了解了研究抛物线的焦半径，焦点弦和通径这对我们解决抛物线中的相关问题有很大的帮助，。（三）在对曲线的问题的处理过程中，我们更多的是从方程的角度来挖掘题目中的条件，认识并熟练掌握数与形的联系。在本节课中，我们运用了数形结合，待定系数法来求解抛物线方程，在解题过程中，准确体现了函数与方程以及分类讨论的数学思想。四、归纳总结