高二数学直线与椭圆的位置关系(一)课件VIP免费

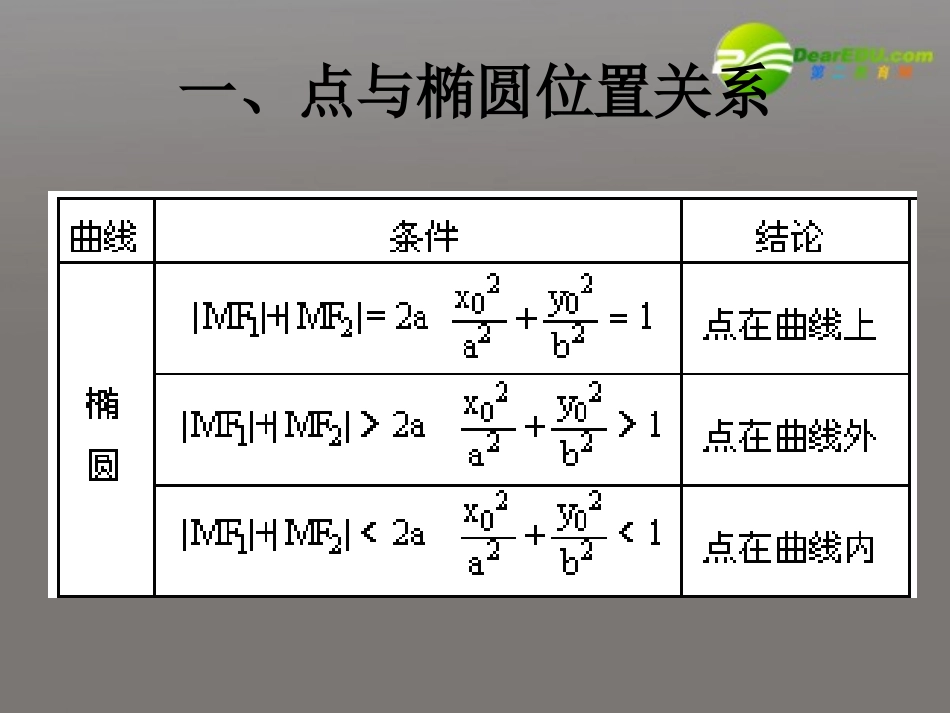
直线与椭圆的位置关系一、点与椭圆位置关系10:2222byaxCByAx，直线和椭圆方程分别为二、直线与椭圆的位置关系：共点。直线和椭圆相离，无公个公共点；直线和椭圆相切，有一个公共点；直线和椭圆相交，有两，则的判别式为若二次方程000010//2/2222cxbxabyaxCByAx则由yoF1F2xyoF1F2xyoF1F2x221.()114425.xyPxyuxy例已知，是椭圆上的点，求的取值范围yoF1F2x代入椭圆方程：解：将xuy125)(14422xux22169288144144250xuxu22(288)4169(14414425)0uu由1313u1313yx22144169(25)0uu2169u222.4112xyyxmm例已知椭圆及直线，（）当直线与椭圆有公共点时，求的范围；（）求被椭圆截得的最长弦所在的直线方程。xyO121代入椭圆将解：mxy)1(01)(422mxx012522mmxx直线与椭圆有公共点，0)1(20422mm2525m点时，直线与椭圆有公共所以当2525m::(,)0lykxbCfxy三、直线与曲线相交所得的“弦长”公式:代入圆的方程将bkxy20,(0)AxBxCA),(),,(2211yxByxA设221221)()(||yyxxAB则),(2211bkxybkxy2212221)()(||xxkxxAB2212)(1xxk2122124)(1xxxxk21||kA弦长公式221()4BCkAA22241BACkA222.4112xyyxmm例已知椭圆及直线，（）当直线与椭圆有公共点时，求的范围；（）求被椭圆截得的最长弦所在的直线方程。xyO121AB(2)yxm解：将代入椭圆012522mmxx由弦长公式得：||AB245522m5102||0maxABm时，当xy此时，直线方程为222420(1)115mm21||kA223.142369.xyM例已知椭圆的弦AB被点（，）平分，求此弦所在直线方程.036)42(4)21(16)41(222kxkkxk4)41(2)21(1620221kkkxxxM.21k解得，得由1936)4(222yxxky.AxyOMB)4(21xky在，设：由题意知直线斜率存解法082)4(212:yxxy即所以所求直线方程为223.142369.xyABM例已知椭圆的弦被点（，）平分，求此弦所在直线方程.AxyOMB1122()()AxyBxy解法2：设，，，，221122221[1]3691[2]369xyxy则09))((36))((]2[]1[21212121yyyyxxxx得：由21212121369yyxxxxyy即.212241MMAByxk四.与弦中点有关的问题的解法：“设点平方差”221434xyCmlyxmC例4.已知椭圆方程为：，试确定的取值范围，使得对于直线：，椭圆上有不同的两点关于该直线对称。nxy41方程为：ABlABlM解法1：设、关于直线对称，且直线交于，AB则由已知可设直线]1[0481681322nnxxy消nxymxy414解方程组)(174mnxm1344122yxnxy解方程组AxyOB..lM13)16169(42m1313213132m1342n即AxyOB..lM在椭圆上、又BA0)4816(13464]1[22nn式的mn413134221nxxxmnmn134)(174]1[0481681322nnxxy消112200()()()AxyBxyABlMxy解法2：设，，，，与的交点，AxyOB..lM]2[134]1[13422222121yxyx则2121212143]2[]1[yyxxxxyy得：由]3[300xy]4[400mxylM又)3(]4][3[mmM，解得联立414300yx在椭圆内在椭圆上、MBA13)3(4)(22mm.1313213132m解得221434xyCmlyxmC例4.已知椭圆方程为：，试确定的取值范围，使得对于直线：，椭圆上有不同的两点关于该直线对称。22221.1,14,,xyyxbbABOAOB已知椭圆方程为直线与椭圆交于，且求椭圆方程。巩固练习22221(0)(),xyabABabmABxAB2.椭圆，一弦中点的横坐标为定值不与轴垂直求证：的中垂线必过定点并求这个定点的坐标。22221.1,14,,xyyxbbABOAOB已知椭圆方程为直线与椭圆交于，且求椭圆方程。AxyOB),(),,(...