高二数学直线与椭圆位置关系课件VIP免费

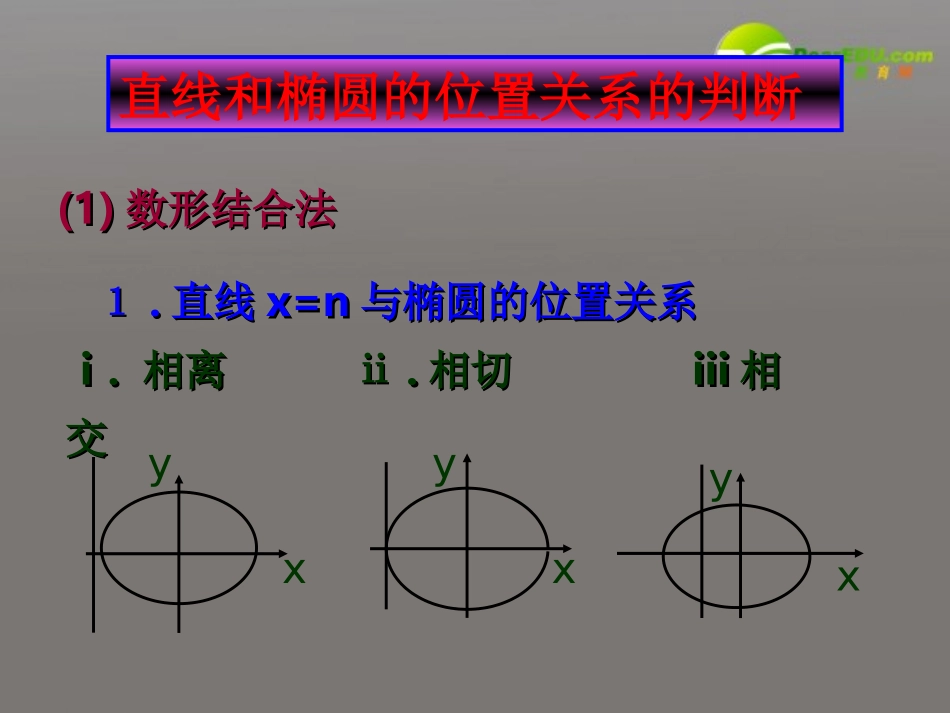
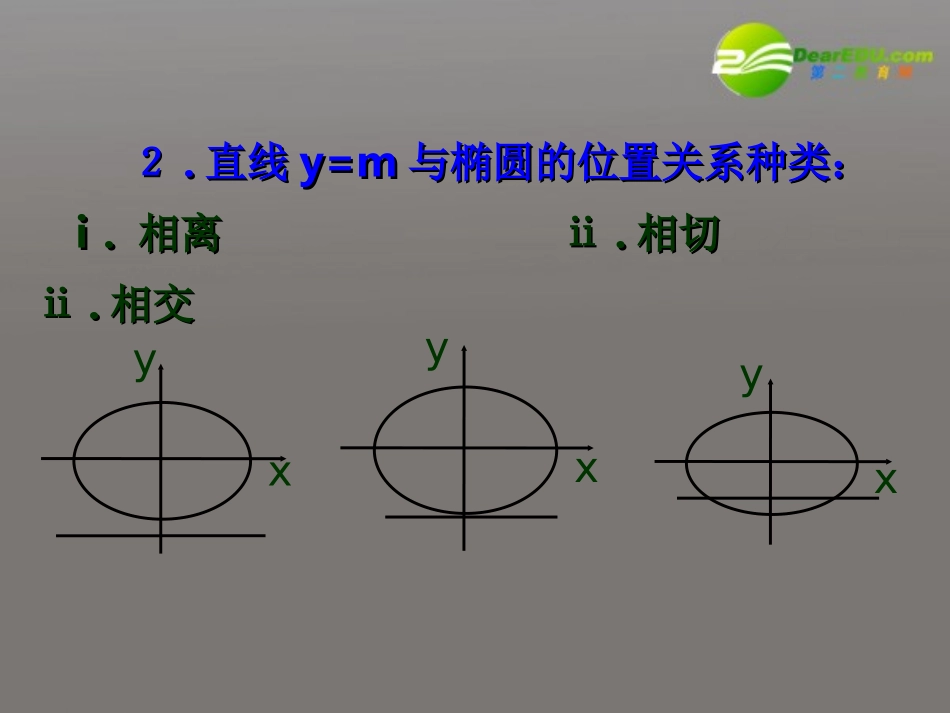
直线与椭圆的位置关系１１..直线直线x=nx=n与椭圆的位置关系与椭圆的位置关系ⅰⅰ..相离ⅱ相离ⅱ..相切相切iiiiii相相交交(1)(1)数形结合法数形结合法xyxyxy直线和椭圆的位置关系的判断２２..直线直线y=my=m与椭圆的位置关系种类：与椭圆的位置关系种类：ⅰⅰ..相离ⅱ相离ⅱ..相切相切ⅱⅱ..相交相交xyyxyxxyxy３.直线y=kx+b与椭圆的位置关系种类：ⅰ.相离ⅱ.相切ⅱ.相交xy2222xy+=1ab椭圆的标准方程为：20AxBxCyx消去则得到关于的一元二次方程（2）判别式法要具体判断出直线和圆的关系，应该将两个方程式联立．算判别式△＞０：相交于两点；△＝０：相切；△＜０：相离．3．直线的斜率为k，被圆锥曲线截得弦AB两端点坐标为（x1,y1）、（x2,y2），则有弦长公式：｜｜△akyyyykyykxxxxkxxkAB221221221221221221214)()1(1||)1(14)(1||1||•例一已知椭圆及直线．•（１）当直线和椭圆有公共点时，求实数的取值范围；•（２）求椭圆截得的最长弦所在的直线方程．•分析：用方程组解的情况来判断，从方程角度看，主要是由一元二次方程根的判别式•解１）解方程组•消去整理得2241xyyxmm0,1422mxyyxy012522mmxx.1620)1(204222mmm，例题应用例题应用•（１）•（２）由韦达定理得，•弦长，•当时，L取得最大值为，此时直线方程为•．515222121mxxmxx221212222L=(1+k)(x+x)-4xx4m4(m-1)2=2-=10-8m25550mxy.2525,0162002mm解之得得由例２.中心在原点一个焦点为的椭圆的截直线所得弦的中点横坐标为，求椭圆的方程．23xy21)50,0(1F分析：分析：根据题意可设椭圆的标准方程，根据题意可设椭圆的标准方程，与直线方程连里解方程组，利用中点公式求与直线方程连里解方程组，利用中点公式求得弦的中点的横坐标，最后解关于的方得弦的中点的横坐标，最后解关于的方程组即可．程组即可．,ab解：设所求椭圆的方程为由得①把直线方程代入椭圆方程，整理得设弦的两个端点为，，则由根与系数的关系得又中点的横坐标为．由此得12222byax)50,0(F5022ba0)4(12)(222222abxbxba),(11yxA),(22yxB22221912babxx21223ba25,7522ba1257522xy.故所求的椭圆方程为:2213(2,1)164xyM过椭圆内一点例引一条弦直线方程。平分，求这条弦所在的，使弦被点M解①、②得：解①、②得：[分析]本题和例2有相似之处，可仿其解法进行。由于本题的实质是求出直线的斜率，在所给的条件下求直线的斜率的方法较多，故本题的解法较多。例４已知椭圆与直线相交于两点，是的中点．若，斜率为（Ｏ为原点），求椭圆方程．122nymx1yx22ABABccABoc22分析：本例是一道综合性比较强的问题，求解本题要利用中点公式求出点坐标，从而得的斜率，另外还要用到弦长公式：2121ABkxx解：由方程组1122yxnymx消去整理得：y012)(2nnxxnm112233(,)(,)(,)AxyBxyCxy设、、1212121212120021,,222()2,,22nnxxxxmnmnnmyyxxmnmnxxyynmxymnmn则22mn则由题设得:22212121221(1)()424(1)2()22ABkxxkxxxxnnmnmn又即：1nmmnnm②①解①②得.32,31nm132322yx所求的椭圆方程为