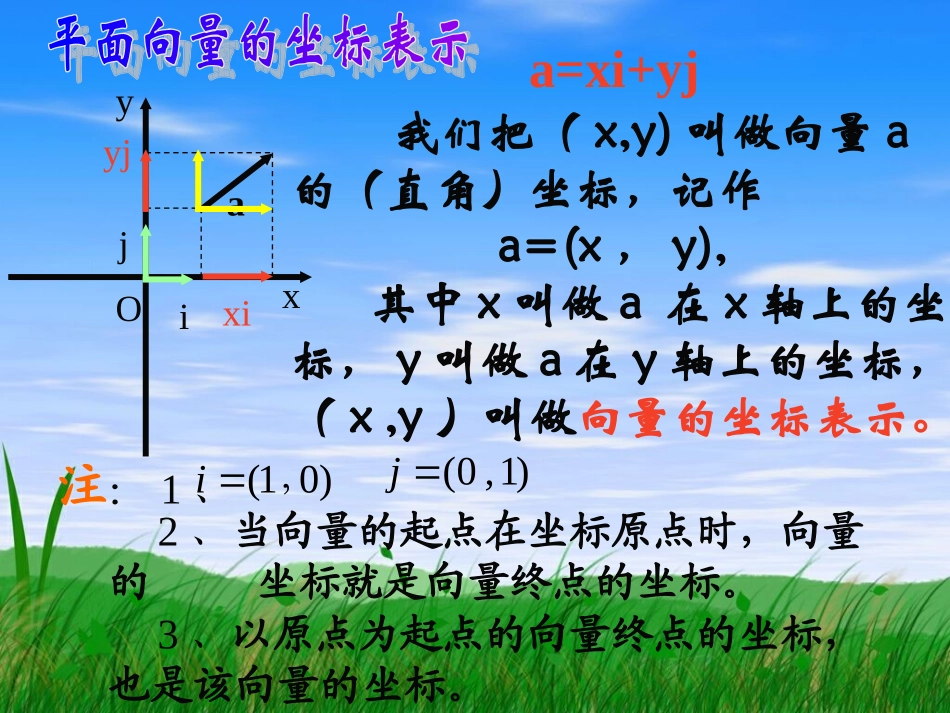
学习目标:1、平面向量的坐标表示与平面向量基本定理的关系。2、平面向量的坐标是如何定义的?3、平面向量的运算有何特点?我们把(x,y)叫做向量a的(直角)坐标,记作a=(x,y),其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标,(x,y)叫做向量的坐标表示。ayjiOxxiyja=xi+yj注:1、)01(,i)1,0(j2、当向量的起点在坐标原点时,向量的坐标就是向量终点的坐标。3、以原点为起点的向量终点的坐标,也是该向量的坐标。平面向量的坐标运算OxyijaA(x,y)a1.以原点O为起点作,点A的位置由谁确定?aOA由a唯一确定2.点A的坐标与向量a的坐标的关系?两者相同向量a坐标(x,y)一一对应概念理解3.两个向量相等的充要条件,利用坐标如何表示?2121yyxxba且yxOyxjA(x,y)a如图,在直角坐标平面内,以原点O为起点作OA=a,则点A的位置由a唯一确定。设OA=xi+yj,则向量OA的坐标(x,y)就是点A的坐标;反过来,点A的坐标(x,y)也就是向量OA的坐标。因此,在平面直角坐标系内,每一个平面向量都可以用一对实数唯一表示。i例1如图,用基底i,j分别表示向量a、b、c、d,并求出它们的坐标。jyxOiaA1AA2bcd解:由图可知a=AA1+AA2=2i+3j,∴a=(2,3)同理,b=-2i+3j=(-2,3)c=-2i-3j=(-2,-3)d=2i-3j=(2,-3)练习:已知向量a=b,并且a=(x+3,2-y)、b=(y+2,x-3),求实数x,y的值。解:因为:a=b所以:(x+3,2-y)=(y+2,x-3)3223xyyx即:32yx解得:已知,你能得出,,的坐标吗?11a=(x,y)22b=(x,y)a+b-abλa已知,a=(x1,y1),b=(x2,y2),则a+b=(x1i+y1j)+(x2i+y2j)=(x1+x2)i+(y1+y2)j即a+b=(x1+x2,y1+y2)同理可得a-b=(x1-x2,y1-y2)两个向量和与差的坐标分别等于这两个向量相应坐标的和与差。加、减运算法则已知a=(x,y)和实数λ,那么λa=λ(x,y)即λa=(λx,λy)实数与向量的积的坐标等用这个实数乘以原来向量的相应坐标。数乘向量坐标法则例2、设解:,,,)3,2(,)2,3(bababa求。ba23bababa23)6,4()6,9();12,5();1,5()3,2()2,3()3,2()2,3();5,1()3,2(2)2,3(3练习:已知向量a、b的坐标,求a+b,a-b的坐标。)1,5(),4,2()1(ba)3,1(),5,3()2(ba)3,5(),3,5()3(ba)1,0(),0,2()4(ba解:)14,52()1(ba)5,3()35,13()2(ba)33,55()3(ba)10,02()4(ba)2,8()2,2()1,2(附加练习结论:一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标。yxOB(x2,y2)A(x1,y1)如图,已知A(x1,y1),B(x2,y2),则AB=OB-OA=(x2,y2)-(x1,y1)=(x2-x1,y2-y1))5,4(),2,3()1(NM)0,3(),3,0()3(NM)5,3(),3,5()2(NM)0,2(),0,5()4(NM解:)3,1()35,53()2(MN)30,03()3(MN)00,52()4(MN)8,8()3,3()0,7(练习:已知点M、N的坐标,求、的坐标。MNNM52,43NM53,35NM03,30NM00,25NM)3,1()8,8()3,3()0,7((1)(43,52)MN�例5已知平行四边形ABCD的三个定点A、B、C的坐标分别为(-2,1)、(-1,3)、(3,4),求顶点D的坐标练习:已知ABCD的三个顶点A(-1,-2)、B(3,-1)、C(3,1)求顶点D的坐标。解:设顶点D的坐标为(x,y)因为点A(-1,-2)、B(3,-1)、C(3,1)所以:)21,13(AB)1,4()1,3(yxDC:,得由DCAByx113401yx所以:顶点D的坐标为(-1,0)。yxoABCD变题已知平行四边形的三个顶点A(-1,-2)、B(3,-1)、C(3,1),求顶点D的坐标。课堂小结1、向量的坐标表示2、向量关系的坐标表示3、向量的坐标运算课外作业学习指导P49~50A组:2、3、4、5