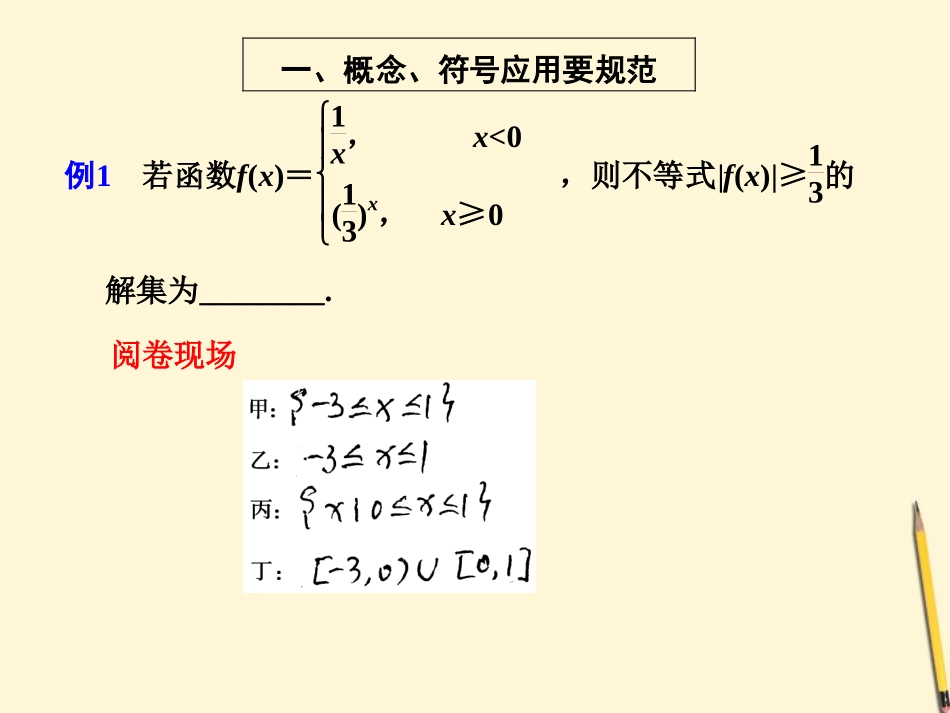
第2讲答题规范教你规范答题少丢分在高考试卷的批阅中,学生因答题不规范而造成的丢分现象是屡见不鲜的.要在高考中不丢分或少丢分,考生们必须从答题规范上下功夫.作为有着多年阅卷经验和教学经验的老师,从答题规范的角度,为考生答题的策略、答题中常见的问题与解决方法,进行点评,希望能对学生增分有帮助.一、概念、符号应用要规范例1若函数f(x)=1x,x<0(13)x,x≥0,则不等式|f(x)|≥13的解集为________.阅卷现场失分原因与防范措施失分原因:(1)概念不清,我们知道,分段函数要分段求,也就是要根据定义域分类讨论,而分类讨论的结果取并集.(2)本题要求是求不等式的解集.解集必须用集合或是区间的形式表述.(3)符号运用不规范.集合表示不能漏掉代表元素.区间表示能合并的要合并.防范措施:(1)要认真审题、找出分类标准,做到不漏解.(2)注意规范运用数学符号.解析(1)当x<0时,由|f(x)|≥13⇒x<0|1x|≥13⇒-3≤x<0.(2)当x≥0时,由|f(x)|≥13⇒x≥0|(13)x|≥13⇒x≥0(13)x≥13⇒0≤x≤1.∴不等式|f(x)|≥13的解集为{x|-3≤x≤1},∴应填[-3,1].答案[-3,1]正解二、结论表述要规范例2在正月十五的庙会上,有人在玩抽奖的游戏.袋中有两白、两红四个球,假设每个球被抽到的概率是均等的.(1)若一次抽两球,问共有哪几种不同的抽法?(2)若一次抽到的两球均为红球,则获奖,问获奖率有多大?阅卷现场失分原因与防范措施失分原因:从本考生的解答过程看,也不是不会做,或者没有思路,关键在于结论的表述不规范.(1)是问有哪几种不同的抽法,因而应将6种不同的方法列举出来.(2)是问中奖率,通常应以百分率的形式回答.防范措施:对于此类问题的解答,一是要认真审题,看清题目要求;二是要分清概念之间的区别,避免混用.正解解(1)设两个白球为B1,B2;两个红球为H1,H2.………1分一次抽两球,可以是{B1,B2},{B1,H1},{B1,H2},{B2,H1},{B2,H2},{H1,H2};………………………………6分所以共有6种不同的抽法.…………………………………7分(2)设“获奖”这一事件计为A.……………………………8分“获奖”所包含的基本事件共有一种,即{H1,H2}.10分∴P(A)=16.…………………………………………………13分∴获奖率约为16.7%.………………………………………14分评分细则(1)第(1)问,只写出抽取方法6种,没有列举,给2分;正确列举出了所有可能,没有总结性语言扣1分.(2)第(2)问,只写出获奖率,过程不全的给2分;概率正确,没有转化为百分率的扣1分.(3)步骤不规范,不完整的,扣除本步骤分.三、书写格式要规范例3在如图所示的几何体中,四边形ABCD是正方形,MA⊥平面ABCD,PD∥MA,E、G、F分别为MB、PB、PC的中点,且AD=PD=2MA.(1)求证:平面EFG⊥平面PDC;(2)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.阅卷现场失分原因与防范措施失分原因:本题在解答过程中,失分的主要原因是格式不规范.推理条件不充分、缺步漏步现象严重,造成失分.防范措施:解题过程要表达准确、格式要符合要求.每步推理要有根有据.计算题要有明确的计算过程,不可跨度太大,以免漏掉得分点.引入数据要明确、要写明已知、设等字样.要养成良好的书写习惯.正解(1)证明因为MA⊥平面ABCD,PD∥MA,所以PD⊥平面ABCD,又BC⊂平面ABCD,所以PD⊥BC.………………………………………………1分因为四边形ABCD为正方形,所以BC⊥DC.……………2分又PD∩DC=D,BC⊥平面PDC,………………………3分又GF∥BC,所以GF⊥平面PDC,………………………5分又GF⊂平面EFG,所以平面EFG⊥PDC.………………7分(2)解因为PD⊥平面ABCD,不妨设MA=a,则PD=AD=2a,所以VP—ABCD=13S正方形ABCD·PD=83a3.………………………9分因为DA⊥平面MAB,且PD∥MA,所以DA即为点P到平面MAB的距离,所以三棱锥VP—MAB=13×12×a×2a×2a=23a3.…………11分所以VP—MAB∶VP—ABCD=1∶4.……………………………14分评分细则(1)在第(1)问中,若缺少线面垂直的条件,则本步不给分.性质或判定的条件不充分的都应适当扣分.(2)在计算过程中,缺少必要的说明,要适当扣...