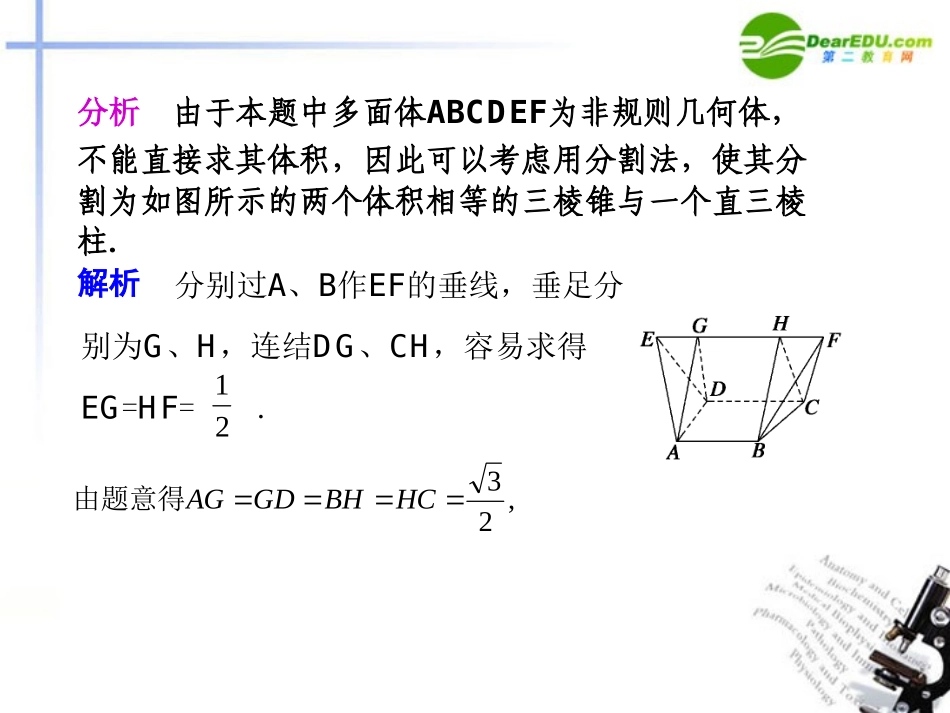
备课资讯17求几何体体积的常用方法一、分割法对于给出的一个不规则的几何体,不能直接套用公式,常常需要运用分割法,按照结论的要求,将原几何体分割成若干个可求体积的几何体,然后再求和.【例1】如右图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为.分析由于本题中多面体ABCDEF为非规则几何体,不能直接求其体积,因此可以考虑用分割法,使其分割为如图所示的两个体积相等的三棱锥与一个直三棱柱.解析分别过A、B作EF的垂线,垂足分别为G、H,连结DG、CH,容易求得EG=HF=.21,23HCBHGDAG由题意得.32221221213112212112221BHCAGDBHCFAGDEABCDEFBHCAGDVVVV,SS本题还可以这样来分割:取EF的中点P,则多面体ABCDEF分割成正四面体ADEP、PBCF和正四棱锥P—ABCD,也易于计算.点评二、补形法利用平移、旋转、延展或对称等手段,将原几何体补成便于求体积的几何体,如正方体、长方体等.【例2】四面体S—ABC的三组对棱分别相等,且依次为25、13、5,求该四面体的体积.分析由三条对棱相等,易联想到长方体的三组相对的面上的对角线长相等,因此可将四面体补成一个长方体来解决.解析将四面体“补”成如图所示的长方体,使四面体对棱分别为长方体相对面的对角线.设长方体的三边分别为x,y,z,所以V四面体=V长方体-4VD—SAB=V长方体-4··V长方体=V长方体=8.,3,2,4,5,)13(,)52(222222222zyxxzzyyx解得则6131点评本题是通过将四面体的四个面向外拓展补为长方体,则问题转化为求一个长方体和四个相等的且有三个直角的三棱锥,再利用间接法求得最后的结果.三、等积转换法“等积转换法”是针对当所给几何体的体积不能直接套用公式或涉及的某一量(底面积或高)不易求解时,可以转换一下几何体中有关元素的相对位置进行计算,该方法尤其适用于求三棱锥的体积.【例3】在边长为a的正方体ABCD—A1B1C1D1中,M、N、P分别是棱A1B1、A1D1、A1A上的点,且满足A1M=A1B1,A1N=2ND1,A1P=A1A,如图,试求三棱锥A1—MNP的体积.2143分析若用公式V=Sh直接计算三棱锥A1—MNP的体积,则需要求出△MNP的面积和该三棱锥的高,两者显然都不易求出,但若将三棱锥A1—MNP的顶点和底面转换一下,变为求三棱锥P—A1MN的体积,显然就容易解答了.解析31MNAPMNPAVV11.241433221213121313111aaaaPANAMA点评转换顶点和底面是求三棱锥体积的一种常用的方法,也是求后面要学习到的求点到平面距离的一个理论依据,相应的方法叫等积法.四、还原图形法此类题主要是没有直接给出几何体,而是给出了几何体的三视图,求体积时一般需要根据三视图还原成直观图,再进行解答.【例4】下图是一个几何体的三视图,根据图中所标的数据求这个几何体的体积.分析本题题设中三视图已经给出,欲求原几何体的体积,需根据“长对正、高平齐、宽相等”的原则将三视图还原成直观图.返回解析由三视图可知这个几何体是由一个三角形旋转得到的几何体,如右图,△ABC绕着过点B且垂直于BC的直线旋转一周得到的几何体即为原几何体,其体积是圆台的体积减去圆锥的体积.因为圆台的上、下底面的半径分别是BC=1、OA=2,且高BO=3,故所求几何体的体积V=V圆台-V圆锥=7π-4π=3π.点评由三视图还原成几何体时,要注意三视图与原几何体之间的各数据的对应关系.