河南省洛阳铁一中高三数学正态分布二 课件VIP免费

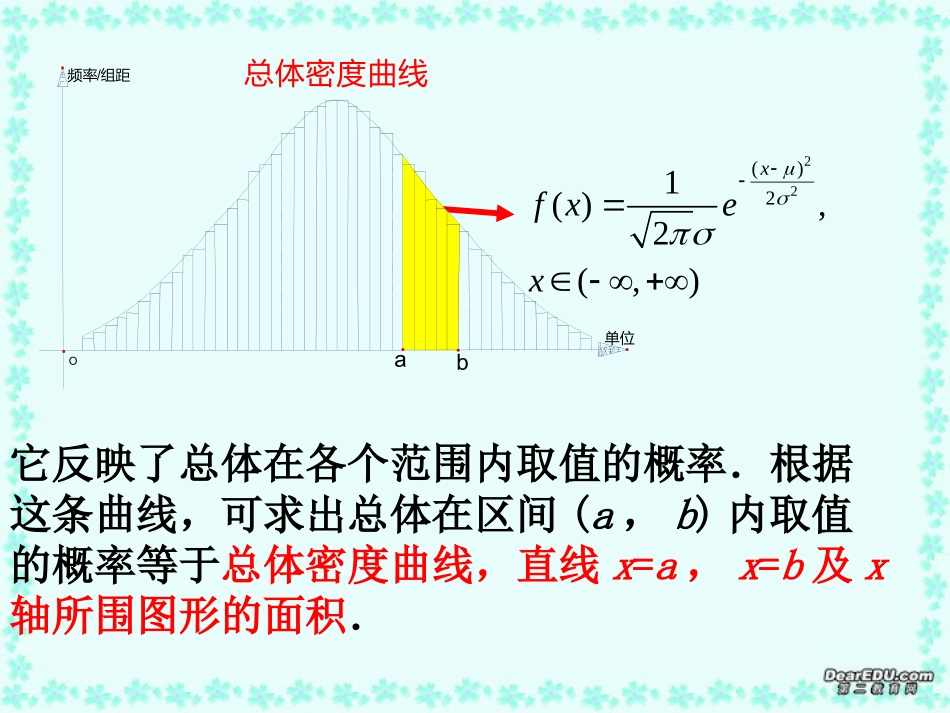
正态分布二它反映了总体在各个范围内取值的概率．根据这条曲线，可求出总体在区间(a，b)内取值的概率等于总体密度曲线，直线x=a，x=b及x轴所围图形的面积．22()21(),2(,)xfxex总体密度曲线b单位O频率/组距a1.标准正态总体N(0,1)的概率问题:表中，相应于的值是指总体取值小于的概率，即：0x0x)(0x,00xxPx如图中，左边阴影部分：由于标准正态总体在正态总体的研究中有非常重要的地位，已专门制作了“标准正态分布表”见p58。1,0N由于标准正态曲线关于轴对称，表中仅给出了对应于非负值的值。y0x0x如果，那么由下图中两个阴影部分面积相等知：00x.100xx利用这个表，可求出标准正态总体在任一区间内取值的概率。21,xx12xxp即可用如图的蓝色阴影部分表示。公式：(12)(2)(1)(2)[1(1)](2)(1)10.97720.841310.8185Px例如：2.非标准正态总体的概率问题:-2(,),(),()()()NFxPxFxx若则的分布函数用表示且有一般的正态总体N(μ,σ2）均可以化成标准正态总体N（0，1）来进行研究。331(3)()(1)0.84132F例如：对于正态总体N(1,4)来说,取值小于的概率例1：分别求正态总体N（μ，σ2）在（μ－σ，μ＋σ）；（μ－2σ，μ＋2σ）；（μ－3σ，μ＋3σ）内取值的概率。2()()[](1),()()[](1),(,)(,)()()(1)(1)(1)[1(1)]2(1)120.841310.683FFNFF解：正态总体在内取值的概率为22(,)(2,2)(2)(2)(2)(2)0.954(,)(3,3)(3)(3)(3)(3)0.997NFFNFF同理，正态总体在内取值的概率为正态总体在内取值的概率为区间取值概率（μ－σ，μ＋σ）68.3%（μ－2σ，μ＋2σ）95.4%（μ－3σ，μ＋3σ）99.7%小概率事件的含义:发生概率一般不超过5％的事件，即事件在一次试验中几乎不可能发生1.~(0,1)1(2.35)21.24);(3)(||1.54).NPPP练习设离散型随机变量，求值：（）；（）（22.(500,100),2500010000N假设某市今年高考考生成绩服从正态分布现有名考生，计划招生名.试估计录取分数线.小结：（1）标准正态分布的概率计算；（2）非标准正态分布的概率计算；（3）正态分布的应用。