高中数学(抛物线)课件3 北师大版选修2-1 课件VIP免费

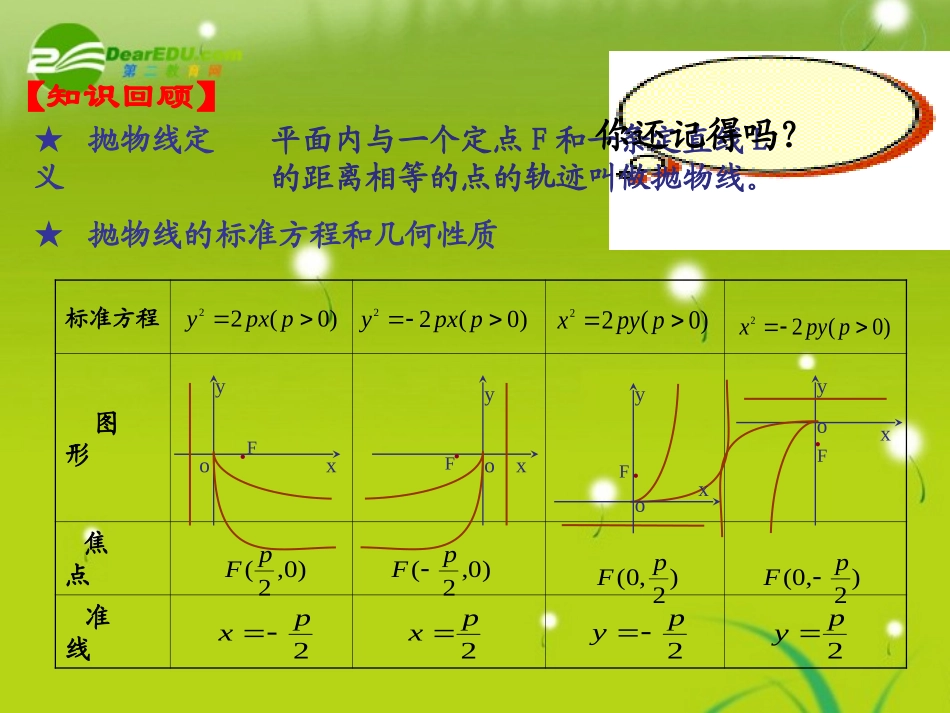
抛物线复习课抛物线复习课【知识回顾】标准方程图形焦点准线)0(22ppxy)0(22ppyxxyoF..xyFo)0,2(pF.yxoF2px)2,0(pF.xoyF2py)0(22ppxy)0,2(pF2px)0(22ppyx)2,0(pF2py★抛物线定义★抛物线的标准方程和几何性质平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫做抛物线。你还记得吗？1.抛物线的焦点坐标是（）。(A)(B)(C)(D))4,0(m)4,0(m)41,0(m)41,0(m)0(12mxmyxyoxyoyxoyxo12222ybxa)0(02babyax【训练一】AD2.坐标系中，方程与的曲线是（）(A)(B)(C)(D)3.动点P到直线x+4=0的距离减它到M(2,0)的距离之差等于2，则P的轨迹是，其方程为。4.过抛物线的焦点作直线交抛物线于两点，如果那么为。抛物线y2=8xxy42),(),(2211yxByxA、,621xxAB8l1l2【例题1】AMN6,3,17BNANAMBAMN分析：1.如何选择适当的坐标系。2.能否判断曲线段是何种类型曲线。3.如何用方程表示曲线的一部分。如图所示，直线L1与L2相交于M点L1⊥L2，N∈L2,以A,B为端点的曲线段C上的任一点到L1的距离与到点N的距离相等，为锐角三角形，,建立适当坐标系,求曲线C的方程。l1l2AMN6,3,17BNANAMyxD解法一：1,22NCACNRtAC中，)0,2(,4为则NMN422pp得由图得，），为（221A），为（244BCBAMN曲线段C的方程为：)0,41(82yxxy即抛物线方程：xy823,ANADMCACMRt如图所示，直线L1与L2相交于M点L1⊥L2，N∈L2,以A,B为端点的曲线段C上的任一点到L1的距离与到点N的距离相等，为锐角三角形，,建立适当坐标系,求曲线C的方程。建立如图所示的直角坐标系，原点为O(0,0)O，l1l2AMN6,3,17BNANAMyxDCBAMN42,或得p解法二：)0(22ppxy设抛物线方程：)22,23(pA)23(28ppNAxxAMN为锐角三角形，43223pppp；即得所以曲线段C的方程为：)0,41(82yxxy如图所示，直线L1与L2相交于M点L1⊥L2，N∈L2,以A,B为端点的曲线段C上的任一点到L1的距离与到点N的距离相等，为锐角三角形，,建立适当坐标系,求曲线C的方程。建立如图所示的直角坐标系，原点为O(0,0)OyxBAMNCD建立如图所示的直角坐标系，原点为解法三：)0,0(M3ANADMCACMRt中，1,22NCACNRtAC中，)02()0,4(,4，为顶点为则QNMNQ)2(82xy抛物线方程为：6,3:BAxx易得曲线段C的方程为：)0,63)(2(82yxxy【例题2】已知抛物线y=x2,动弦AB的长为2，求AB中点纵坐标的最小值。xoyFABMCND解：),(),(),,(2211yxMAByxByxA中点设,2BCADMN,412yypMNBFBCAFAD,)41(2yBFAF2,ABBFAFABF中43,2)41(2yy即)41(2yBCAD【训练二】1.已知M为抛物线上一动点，F为抛物线的焦点，定点P(3,1),则的最小值为（）(A)3(B)4(C)5(D)6MFMPxy422.过点(0,2)与抛物线只有一个公共点的直线有（）（A）1条(B)2条(C)3条(D)无数多条xy82BC)0,1(F3xM.N.M.P.P3.过抛物线的焦点F作一直线交抛物线于P、Q两点，若PF与FQ的长分别是()(A)2a(B)(C)4a(D))0(2aaxy等于q1p1q则p,a21a2yxFPQ4.已知A、B是抛物线上两点，O为坐标原点，若的垂心恰是此抛物线的焦点，则直线AB的方程是：()(A)(B)(C)(D))0(22ppxyAOBOBOA且,pxpx3px23px25ABOF.yxCD【总结】1.灵活应用抛物线的定义解决相关题目2.建立适当的坐标系3.不同标准方程的几何性质是易混点，性质的应用是难点【思考题】在抛物线y2=64x上求一点，使它到直线Ｌ：4x+3y+46=0的距离最短，并求此距离。分析：抛物线上到直线Ｌ距离最短的点，是和此直线平行的切线的切点。yxy2=64x4x+3y+46=0解：∵无实根∴直线与抛物线相离设与4x+3y+46=0平行且与y2=64x相切的直线方程为y=-4/3x+bL·P则由y=-4/3x+by2=64x消x化简得y2+48y-48b=0△=482-4×(-48b)=0∴b=-12∴切线方程为：y=-4/3x-12y=-4/3x-12y2=64x解方程组得x=9y=-24∴切点为P（9，-24）切点P到Ｌ的距离d=234|46)24(394|22∴抛物线y2=64x到直线Ｌ：4x+3y+46=0有最短距离的点为P（9，-24），最短距离为2。