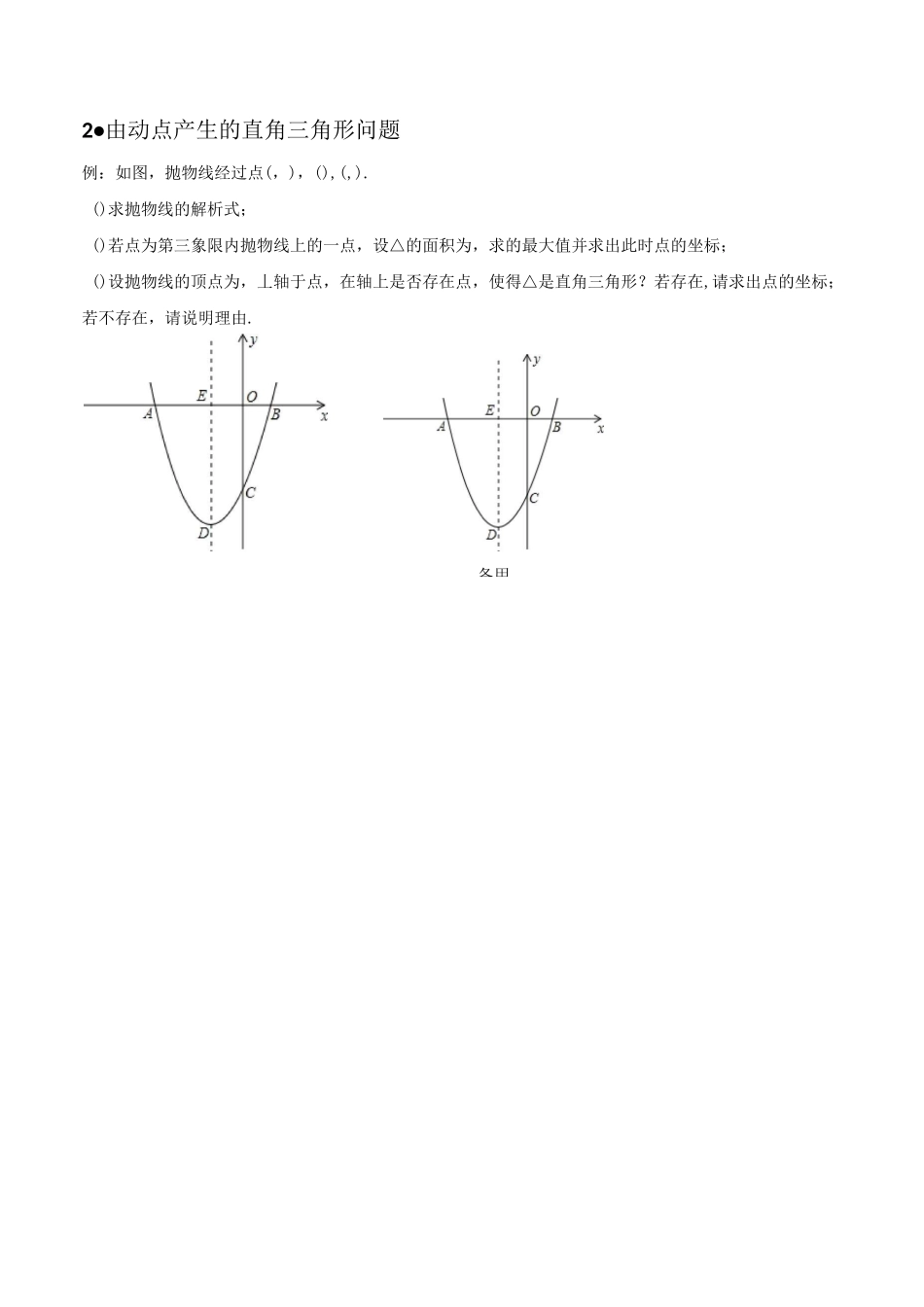
由动点产生的三角形问题、方法规律以及常用知识点、平面直角坐标系中已知一条线段，构造等腰三角形，用的是“两圆一线”分别以线段的两个端点为圆心，线段长度为半径作圆，再作线段的垂直平分线；、平面直角坐标系中已知一条线段，构造直角三角形，用的是“两线一圆”分别过已知线段的两个端点作已知线段的垂线，再以已知线段为直径作圆；、平面内有两点（）（）贝9=,中点的坐标为
、求三角形的面积：（1）直接用面积公式计算；（2）割补法；（3）铅垂高法；、平面直角坐标系中直线1［和直线12：当〃时当丄时・由动点产生的等腰三角形例：如图，抛物线=++经过一、、三点，直线是抛物线的对称轴
（）求抛物线的函数关系式；（）设点是直线上的一个动点，当△的周长最小时，求点的坐标；（）在直线上是否存在点，使厶为等腰三角形，若存在，求出所有符合条件的点的坐标；若不存在，请说明理由
备用2•由动点产生的直角三角形问题例：如图，抛物线经过点(，)，(),(,)
()求抛物线的解析式；()若点为第三象限内抛物线上的一点，设△的面积为，求的最大值并求出此时点的坐标；()设抛物线的顶点为，丄轴于点，在轴上是否存在点，使得△是直角三角形
若存在,请求出点的坐标；若不存在，请说明理由
备用3•由动点产生的等腰直角三角形例：在平面直角坐标系中，现将一块等腰直角三角板放在第一象限，斜靠在两坐标轴上，且点（，）,点（，），如图所示，抛物线经过点
（）求抛物线的解析式；（）在抛物线上是否还存在点（点除外），使厶仍然是以为直角边的等腰直角三角形
若存在,求所有点的坐标；若不存在，请说明理由
、如图，抛物二、实战训练1、如图，在平面直角坐标系xOy中，A(0,2),B(0,6),动点C在直线y=x上
若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是():/H1Z111丿X经过△的三个顶点，已知〃轴，点在轴上，点在轴上，且()求抛
