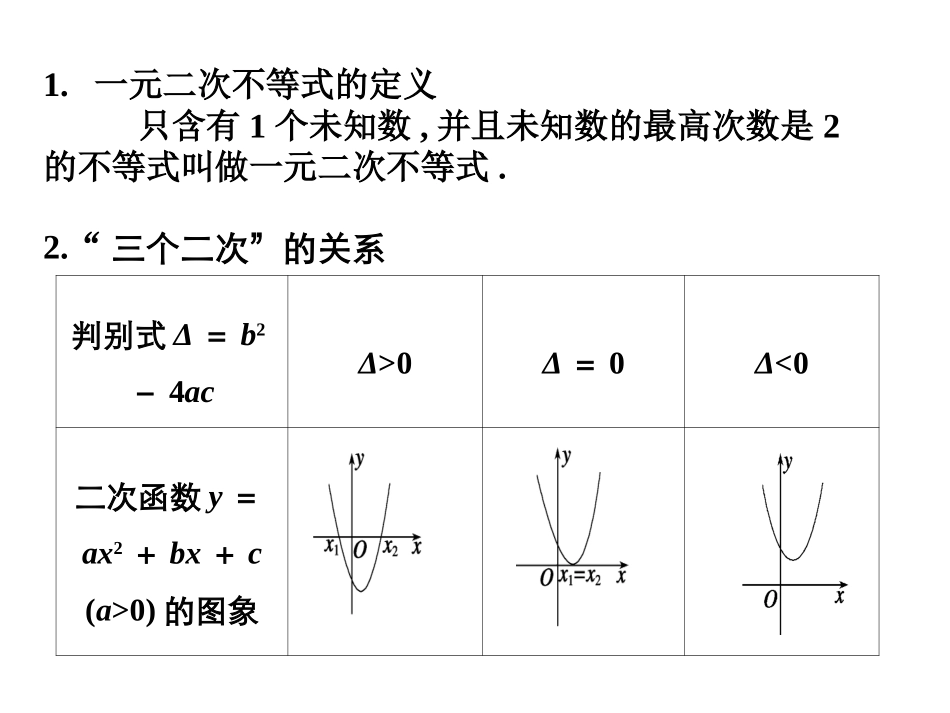
一元二次不等式及其解法2.“三个二次”的关系判别式Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象1.一元二次不等式的定义只含有1个未知数,并且未知数的最高次数是2的不等式叫做一元二次不等式.一元二次方程ax2+bx+c=0(a>0)的根有两相异实根x1,x2(x10(a>0)的解集ax2+bx+c<0(a>0)的解集_______b2a{x|xx2}{x|x≠x1}{x|x∈R}{x|x10Δ=0Δ<03.ab,xaxb0;0xaxb0()()0,0;()()0,0.0;00xaxbxaxbxaxbxaxbxbxaxbxaxbxb≥≥≤≤分式不等式与一元二次不等式的关系设等价于等价于等价于等价于思考辨析判断下面结论是否正确(请在括号中打“√”或“×”)(1)若ax+b>0,则x>-.()(2)不等式-x2-5x+6<0的解集为{x|x<-6或x>1}.()(3)不等式≤0的解集是[-1,2].()(4)若不等式ax2+bx+c>0的解集是(-∞,x1)∪(x2,+∞),则方程ax2+bx+c=0的两个根是x1和x2.()bax-2x+1×√×√(5)若方程ax2+bx+c=0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R.()(6)不等式ax2+bx+c≤0在R上恒成立的条件是a<0且Δ=b2-4ac≤0.()××题型一一元二次不等式的解法【例1】(2014·四川)已知集合A=022xxx,集合B为整数集,则A∩B=()A.2,1,0,1B.1,0,12C.1,0D.0,1【解】由于集合A=022xxx=12xx,而集合B为整数集,在12x范围中的整数有1,0,1,2,故A∩B=2,1,0,1.选A.解下列不等式:(1)2x2+4x+3<0;(2)–3x2–2x+8≤0;(3)8x–1≥16x2.答案:(1)∅(2)(–∞,–2]∪[43,+∞)(3)1{}4练习解一元二次不等式的一般步骤(1)化:把不等式变形为二次项系数大于零的标准形式.(2)判:计算对应方程的判别式.(3)求:求出对应的一元二次方程的根,或根据判别式说明方程有没有实根.(4)写:利用“大于取两边,小于取中间”写出不等式的解集.【例2】已知不等式ax2-3x+6>4的解集为{x|x<1或x>b}.(1)求a,b的值;(2)解不等式ax2-(ac+b)x+bc<0.题型二含参不等式的解法【解】(1)因为不等式ax2-3x+6>4的解集为{x|x<1或x>b},所以x1=1与x2=b是方程ax2-3x+2=0的两个实数根,b>1且a>0.由根与系数的关系,得1+b=3a,1×b=2a,解得a=1,b=2.【例2】已知不等式ax2-3x+6>4的解集为{x|x<1或x>b}.(1)求a,b的值;(2)解不等式ax2-(ac+b)x+bc<0.题型二含参不等式的解法【解】(2)不等式ax2-(ac+b)x+bc<0,可化为x2-(2+c)x+2c<0,即(x-2)(x-c)<0.当c>2时,不等式(x-2)(x-c)<0的解为2<x<c;当c<2时,不等式(x-2)(x-c)<0的解为c<x<2;当c=2时,不等式(x-2)(x-c)<0的解集为∅.所以,当c>2时,不等式ax2-(ac+b)x+bc<0的解集为{x|2<x<c};当c<2时,不等式ax2-(ac+b)x+bc<0的解集为{x|c<x<2};当c=2时,不等式ax2-(ac+b)x+bc<0的解集为∅.练习(1)不等式ax2+bx+c>0的解集为{x|2<x<3},则不等式ax2-bx+c>0的解集为________.(2)解不等式:ax2-(a+1)x+1<0.【答案】(1){x|-3<x<-2}【解】(2)若a=0,原不等式等价于-x+1<0,解得x>1.若a<0,则原不等式等价于x-1a(x-1)>0,解得x<1a或x>1.若a>0,原不等式等价于x-1a(x-1)<0.①当a=1时,1a=1,x-1a(x-1)<0无解;②当a>1时,1a<1,解x-1a(x-1)<0得1a<x<1;③当0<a<1时,1a>1,解x-1a(x-1)<0得1<x<1a.综上所述:当a<0时,解集为xx<1a或x>1;当a=0时,解集为{x|x>1};当0<a<1时,解集为x1<x<1a;当a=1时,解集为∅;当a>1时,解集为x1a<x<1.(2)解不等式:ax2-(a+1)x+1<0.练习解含参数的一元二次不等式时分类讨论的依据(1)二次项中若含有参数应讨论是等于0,小于0,还是大于0,然后将不等式转化为一次不等式或二次项系数为正的形式....