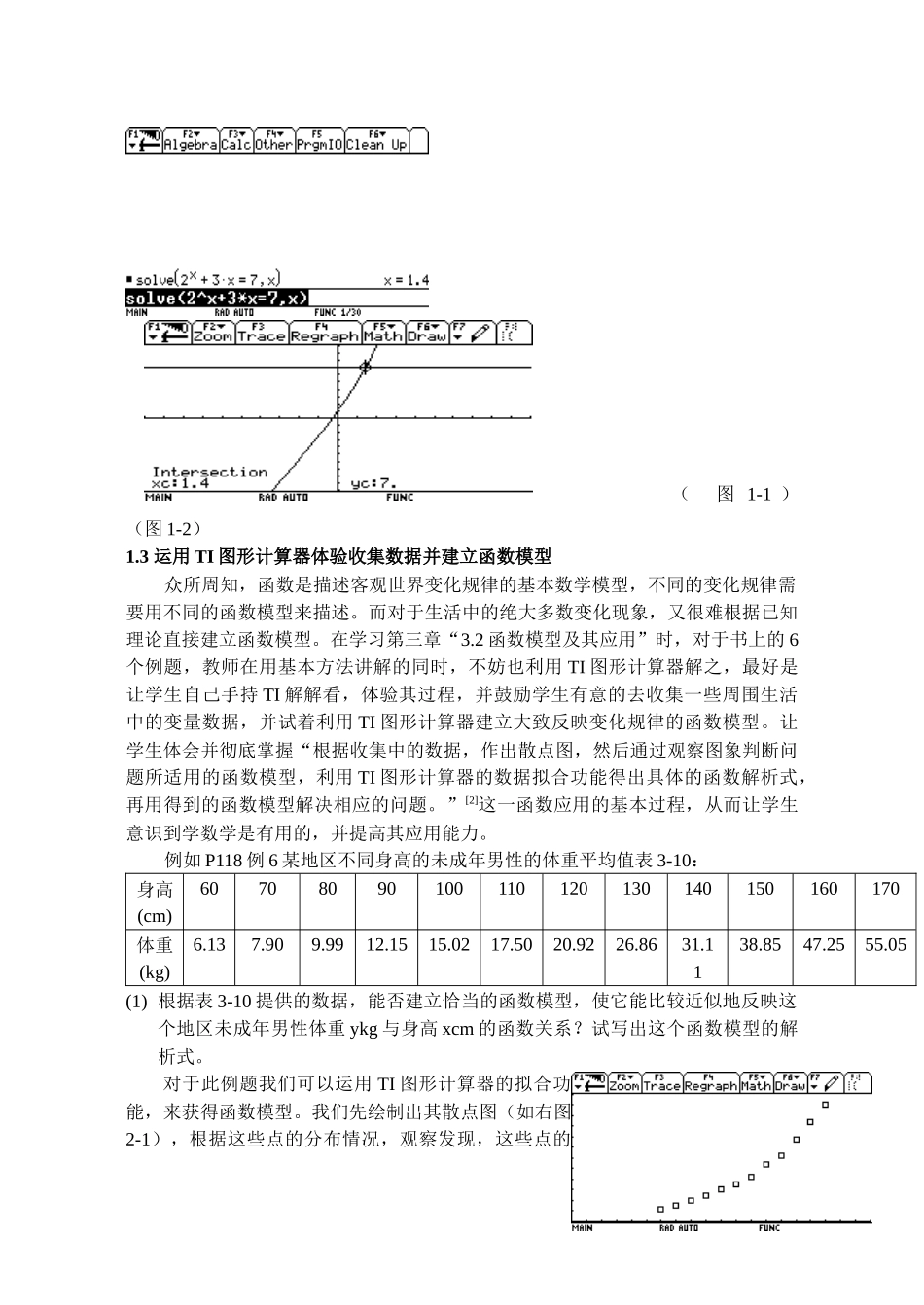
TI图形计算器在高中新课标实验教材数学①中的应用及若干思考四中分校余云娟摘要:随着现代信息技术的广泛应用,TI图形计算器以其特有的优势开始进入数学教育技术领域,它的出现将会对数学课程改革和学生数学学习方式产生巨大的影响。本文主要阐述其在高中数学新课标实验教材数学①中的具体应用,及由此产生的若干思考。关键词:图形计算器;现代教育技术;函数模型;教育观念现代信息技术的广泛应用正在对数学课程内容、数学教学、数学学习等方面产生深刻的影响,《高中数学课程标准》中的课程理念就特别强调“注重信息技术与数学课程的整合”。所谓信息技术与数学课程的整合,就是通过数学课把信息技术和数学教学有机地结合起来,将信息技术与数学课程的教与学融为一体,将技术作为一种工具,提高教与学的效率,改善教与学的效果。TI图形计算器是一种现代手持技术,它具有数据处理功能、函数功能、图形功能、简单编程功能和进行一些数理实验功能,是教学、学习和做数学的强有力工具。它为数学思想提供了可视化的图像,使组织和分析数据容易实现,更重要的是TI图形计算器具有便携性和灵活性,这为数学教学提供了便利。高中数学课程提倡利用信息技术来呈现以往教学中难以呈现的课程内容,“在保证笔算训练的前提下,尽可能使用科学型计算器、各种数学教育技术平台,加强数学教学与信息技术的结合,鼓励学生运用计算机、计算器等进行探索和发现”[1]。正是基于此理念,高中数学新课标实验教材数学①(刘绍学主编)与现代信息技术进行了很好的整合:在第一章函数的基本性质中,教材在P41就给出了“信息技术应用”(用计算机绘制函数图像);在指数函数这节内容中,P67给出了“信息技术应用”(借助信息技术探究指数函数的性质);在第三章“函数的应用”中,P103有一个“信息技术应用”(借助信息技术求方程的近似解);在“3.2函数模型及其应用”中,P122又安排了“信息技术应用”(收集数据并建立函数模型)。这4处的“信息技术应用”都可以用手持TI图形计算器进行教学,学生也可以自己动手实践,积极地参与探究性活动,主动地建构知识,这不仅能增强学生的动手实验能力,还可以使学生有机会体验更为完全及丰富多彩的数学过程有助于促进学生的应用意识和扩展其视野。本文主要分析TI图形计算器在高中数学新课标实验教材数学①中的具体应用,及若干思考,供各位读者参考。1TI图形计算器在数学①中的应用2006年杭州市数学会评选论文1.1运用TI图形计算器绘制图像并探究其性质利用TI图形计算器可以便捷地绘制各种函数图像,对于一些复杂的函数,当其图像难以手动画出时,我们就可以利用TI图形计算器,先转化为“function”模式,直接输入函数表达式,并设定适当的窗口值,就可以很快地绘制出其图像,并且从图像上我们就可以一幕了然的知道其单调性和奇偶性。特别是对于第二章中的“指数函数、对数函数和幂函数”教学,在讲授其图像及性质时,教师可以让学生先自己持TI图形计算器进行探究,通过函数图像变化的动态演示,猜想、归纳、概括出其性质以及不同函数之间的联系与区别。这样让学生自己一步步通过探究获得的知识,既能加深学生对知识点的印象,又能让学生体验知识生成的全过程,从而提高他们的学习兴趣,使他们乐于学、愿意学数学。1.2运用TI图形计算器求方程的近似解数学①第三章“3.1函数与方程”中,教材给出了用二分法求方程的近似解,并给出了求解的具体步骤。其实,我们也可以利用TI图形计算器使用二分法的小程序,得到零点,对于感兴趣的学生,教师不妨也讲一讲。除此之外,不用二分法我们也可以很方便地利用TI图形计算器求出一个方程的近似解或者是函数的零点,例如P105中的“例2借助计算器或计算机用二分法求方程的近似解(精确到0.1)”,下面我们用另外两种方法解之。1.利用TI图形计算器的代数自动求解功能求方程的近似解.先将图形计算器的浮点数设置为2位;选择命令“solve(解方程)”;将方程“”输入计算器,便可以自动求出方程的近似解.(如图1-1)2.TI图形计算器的画图功能求方程的近似解.先将计算器或计算机的浮点数设置为2位;分别将函数“”和“”输入计算器...