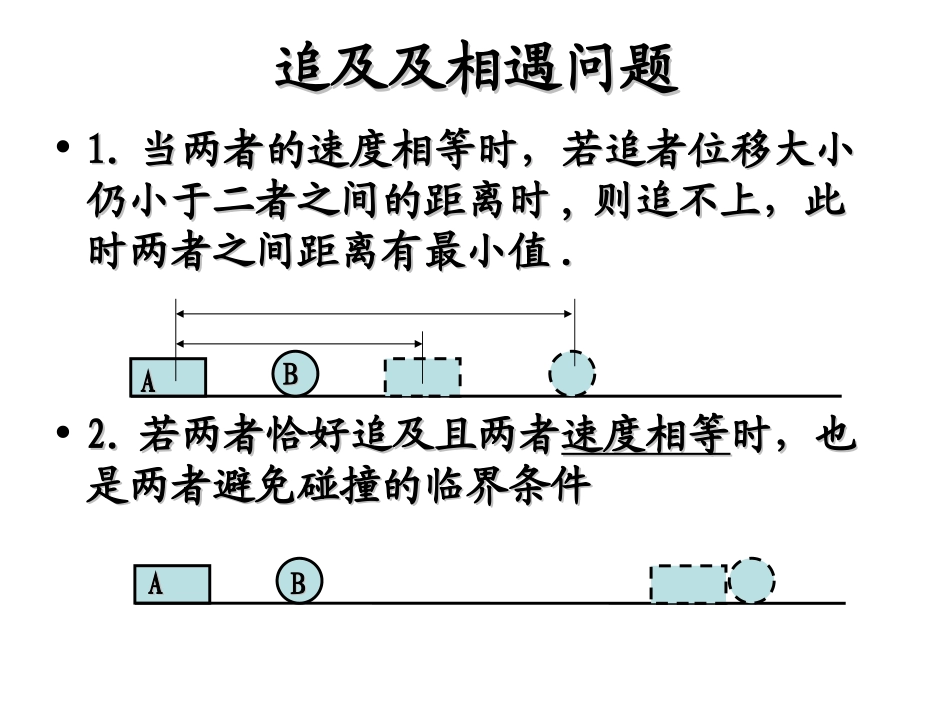
第第77节追及相遇问题节追及相遇问题追及及相遇问题追及及相遇问题•一追及问题一追及问题•追和被追的两物体速度相等是追及问题中追和被追的两物体速度相等是追及问题中能否追上或二者距离具有极值的临界条件能否追上或二者距离具有极值的临界条件..根据两物体的运动情况,追及问题大致可根据两物体的运动情况,追及问题大致可以分为两大类以分为两大类..•第一类:速度大者追速度小者,如匀减速第一类:速度大者追速度小者,如匀减速追匀速,匀速追匀加速追匀速,匀速追匀加速..•1.1.当两者的速度相等时,当两者的速度相等时,若追者位移大小若追者位移大小仍小于仍小于二者之间的距离时二者之间的距离时,,则追不上,此则追不上,此时两者之间距离有最小值时两者之间距离有最小值..•2.2.若两者若两者恰好追及且两者恰好追及且两者速度相等速度相等时,也时,也是两者避免碰撞的临界条件是两者避免碰撞的临界条件追及及相遇问题追及及相遇问题AABBAABB追及及相遇问题追及及相遇问题•3.3.若两者位移相等时追者的速度仍大于被若两者位移相等时追者的速度仍大于被追者的速度,则被追者还有一次追上追者追者的速度,则被追者还有一次追上追者的机会,的机会,这个过程当中这个过程当中速度相等速度相等时两者间时两者间距离有一个距离有一个最大值最大值..AABB追及及相遇问题追及及相遇问题•第二类:速度小者追速度大者,如初速度为第二类:速度小者追速度大者,如初速度为零的匀加速追匀速,匀速追匀减速零的匀加速追匀速,匀速追匀减速..•1.1.当两者速度相等时,二者间有最大距离当两者速度相等时,二者间有最大距离..•2.2.当两者的位移相等时则追上当两者的位移相等时则追上..•二相遇问题二相遇问题•1.1.同向运动的两物体追及时同向运动的两物体追及时即相遇即相遇..•2.2.相向运动的物体当各自发生的位移大小之相向运动的物体当各自发生的位移大小之和等于开始时两物体的距离时即相遇和等于开始时两物体的距离时即相遇..•注:对相遇问题,只需建立位移关系注:对相遇问题,只需建立位移关系..基础练习基础练习•1.1.汽车正以汽车正以10m/s10m/s的速度在平直公路上前的速度在平直公路上前进,突然发现正前方有一辆自行车以进,突然发现正前方有一辆自行车以4m/s4m/s的速度做同方向的匀速直线运动,汽车立的速度做同方向的匀速直线运动,汽车立即关闭油门做加速度大小为即关闭油门做加速度大小为6m/s6m/s22的匀减速的匀减速运动,汽车运动,汽车恰好恰好不碰上自行车,求关闭油不碰上自行车,求关闭油门时汽车离自行车多远门时汽车离自行车多远..•解题思路:汽车的速度大于自行车的速度,解题思路:汽车的速度大于自行车的速度,即二者之间的距离在不断减小,当距离减即二者之间的距离在不断减小,当距离减到零时且二者速度相等时,则能满足题意到零时且二者速度相等时,则能满足题意..•解:取汽车运动的方向为正方向解:取汽车运动的方向为正方向,,已知汽车的速度已知汽车的速度vv00==10m/s,10m/s,自行车匀速行驶的速度自行车匀速行驶的速度vv11==4m/s,4m/s,汽车刹汽车刹车时的加速度车时的加速度aa=-=-6m/s6m/s22,,设关闭油门时汽车离自设关闭油门时汽车离自行车的距离为行车的距离为xx00..•如图如图,,要使汽车恰好不碰上自行车,则有:要使汽车恰好不碰上自行车,则有:•xx00++xx11==xx22…………………(1)…………………(1)•汽车的末速度汽车的末速度vvtt=v=v11…………………(2)…………………(2)•设经过时间设经过时间tt汽车的速度与自行车的速度相等汽车的速度与自行车的速度相等,,则则有有::•vv11t=xt=x11…………………(3)…………………(3)•vvtt=v=v00+at…………………(4)+at…………………(4)•vvtt22-v-v0022=2ax=2ax22…………………(5)…………………(5)•联立方程联立方程(1)(1)、、(2)(2)、、(3)(3)、、(4)(4)、、(5)(5)代入数据代入数据,,解得解得xx00=3m=3m•所以所以,,关闭油门时汽车离自行车的距离为关闭油门时汽车离自行车的距离为3m.3m.xx00xx22xx11基础练习基础练习•2.2.有两辆同样的列车各以有两辆同样的列车各以72km/h72km...