积的乘方 (2)VIP免费

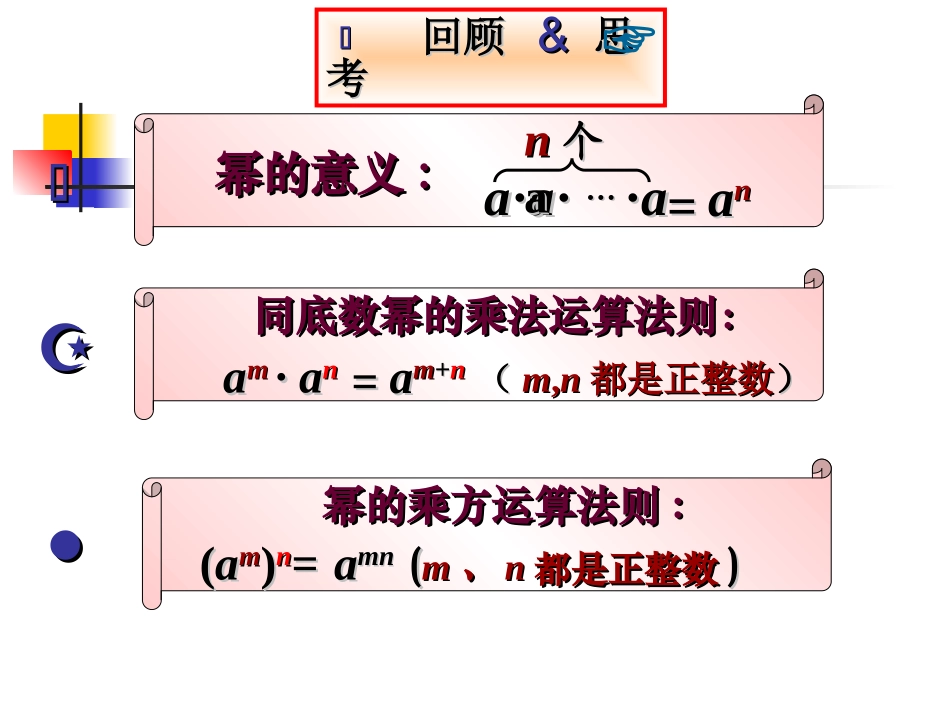
李楼中学梁淑芹8.13积的乘方授课人：贾艳秋回顾与思考回顾回顾&&思思考考☞幂的意义幂的意义::aa··aa··……··aann个个aaaann==同底数幂的乘法运算法则：同底数幂的乘法运算法则：aamm·a·ann==aamm++nn（（mm,,nn都是正整数都是正整数））幂的乘方运算法则幂的乘方运算法则::((aamm))nn==((mm、、nn都是正整数都是正整数))aamnmn探索与交流(1)(ab)3表示什么?2)2(a探索探索&&交流交流(ab)(ab)33==abab··abab··abab==aa··aa··aa··bb··bb··bb==aa33··bb33(2)===(3)===222a22)2(a44aaa2224a222)(2a2222aa猜想猜想((abab))nn==aannbbnn的证明在下面的推导中，说明每一步(变形)的依据：((abab))nn==abab··abab··…………··abab()()=(=(aa··aa·……··……·aa)()(bb··bb·……··……·bb))()()==aann··bbnn．．(())幂的意义幂的意义乘法交换律、乘法交换律、结合律结合律幂的意义幂的意义nn个个ababnn个个aann个个bb((abab))nn==aann··bbnn积的乘方法则上式显示:积的乘方=.((abab))nn==aann··bbnn积的乘方积的乘方乘方的积乘方的积（（mm,,nn都是正整数都是正整数））每个因式分别乘方后的积每个因式分别乘方后的积积的乘方法则积的乘方法则例题解析【【例例11】】计算：计算：(1)(1)(3(3xx))22;;(2)(2)((-22bb))55;;(3)(3)((-22xyxy))44;;(4)(4)(3(3aa22))nn..=3=322xx22==99xx22;;(1)(1)((33xx))22解：解：(2)(2)((-22bb))55=(=(-22))55bb55==-3232bb55;;(3)(3)((-22xyxy))44==((-22xx))44yy44==((-2)2)44xx44yy44(4)(4)(3(3aa22))nn==33nn((aa22))nn==33nnaa22nn。。阅读阅读体验体验☞=16=16xx44yy44；；公式的拓展(abc)(abc)nn=a=ann··bbnn··ccnn怎样证明怎样证明??(abc)(abc)nn=[(ab)=[(ab)··c]c]nn=(ab)=(ab)nn··ccnn==aann··bbnn··ccnn..32)102(（1）（（22））3)43(ab（3）32)23(yx（4）223)21(zxy例题解析【【例例33】】地球可以近似地看做是球体，如果用地球可以近似地看做是球体，如果用V,rV,r分别代表球的体积和半径，那么。地球的半分别代表球的体积和半径，那么。地球的半径约为径约为66××101033千米，它的体积大约是多少立方千米千米，它的体积大约是多少立方千米解：解：阅读阅读体验体验☞334rV334rV34==××(6(6××101033))3334==××6633××101099≈≈9.059.05××10101111((千米千米1111))注意注意运算顺序运算顺序!!随堂练习32332)(3)2(baba222)2()3()2(xxx232324)3()(9nmnm提高练习提高练习计算：计算：(1);(1);(2)(2)21)1(5.022011100100(1)(2)(3)(4)本节课你的收获是什么？幂的意义幂的意义::aa··aa··……··aann个个aaaann==同底数幂的乘法运算法则：同底数幂的乘法运算法则：aamm··aann==aamm++nn幂的乘方运算法则幂的乘方运算法则::((aabb))nn==aannbbnn积的乘方积的乘方==..每个因式分别乘方后的积每个因式分别乘方后的积1、不用计算器，你能很快求出下列各式的结果吗？，2、若n是正整数，且，求的值。3、等于什么？写出推理过程。智能训练：5553210925.045,6nnyxnxy2ndcba1、填空：2、选择：可以写成_____A、B、C、D、3、填空：如果，那么4、计算：拓展训练：点评：要根据具体情况灵活利用积的乘方运算性质（正用与逆用）。______235a_________22372yxyyx13mx13mx13mxmxx312mmx1233yxyxnm__________,nm200320033475.0公式的反向使用试用简便方法计算试用简便方法计算::((abab))nn==aann··bbnn（（mm,,nn都是正整数都是正整数））反向使用反向使用::aann··bbnn==((abab))nn(1)(1)2233××5533;;(2)(2)2288××5588;;(3)(3)((-5)5)1616××((-2)2)1515;;(4)(4)2244××4444××((-0.125)0.125)44;;=(=(22××55))33=10=1033=(=(22××55))88=10=1088=(=(-5)5)××[([(-5)5)××((-2)2)]]1515==-55××10101515;;=[2=[2××44××((-0.125)]0.125)]44=1=144=1.=1.作业习题习题1.61.6——11、、22、、33、、44；；作业作业试一试试一试。。