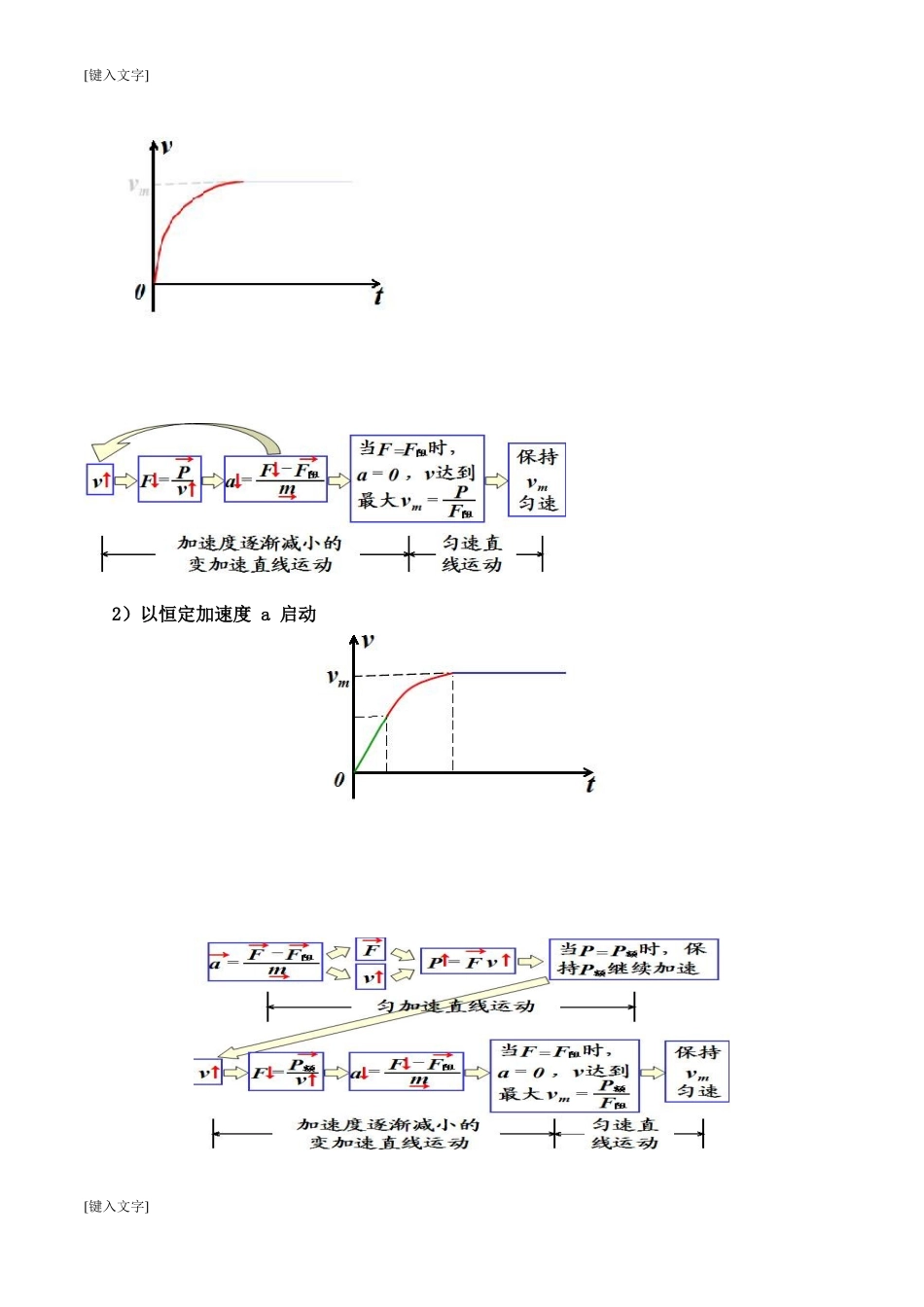
[键入文字]第七章 机械能守恒定律【知识点】:一、功1、做功两个必要因素:力和力的方向上发生位移。2、功的计算:3、正功和负功:①当 o≤a<π/2 时,cosa>0,w>o,表示力对物体做正功。 ② 当 a=π/2 时,cosa=0,w=0,表示力对物体不做功(力与位移方向垂直)。 ③ 当 π/2<a≤π 时,cosa<0,w<0,表示为对物体做负功。4、求合力做功:1)先求出合力,然后求总功,表达式为 W 总=F 合L cosθ(为合力与位移方向的夹角)2)合力的功等于各分力所做功的代数和,即 W 总 =W1+W2+W3+------- 例题、如图 1 所示,用力拉一质量为 m 的物体,使它沿水平匀速移动距离 s,若物体和地面间的摩擦因数为 μ,则此力对物体做的功为( ) A.μmgs B.μmgs/(cosα+μsinα) C.μmgs/(cosα-μsinα) D.μmgscosα/(cosα+μsinα)二、功率1、定义式: ,所求出的功率是时间 t 内的平均功率。 2、计算式: ,其中 θ 是力与速度间的夹角。用该公式时,要求 F 为恒力。 1)当 v 为瞬时速度时,对应的 P 为瞬时功率; 2)当 v 为平均速度时,对应的 P 为平均功率 3)若力和速度在一条直线上,上式可简化为3、机车起动的两种理想模式 1)以恒定功率启动[键入文字] 图 1[键入文字] 2)以恒定加速度 a 启动[键入文字][键入文字]三、重力势能重力势能表达式: 重力做功: (重力做功与路径无关,只与物体的初末位置有关)四、弹性势能 弹性势能表达式: (为弹簧的型变量)五、动能定理(1)动能定理的数学表达式为:(2)动能定理应用要点① 外力对物体所做的总功,既等于合外力做的功,也等于所有外力做功的代数和。② 不管是否恒力做功,也不管是否做直线运动,该定理都成立;对变力做功,应用动能定理更方便、更迅捷。③ 动能定理涉及一个过程,两个状态。所谓一个过程是指做功过程,应明确该过程各外力所做的总功,若物体运动过程中包括几个物理过程,物体的运动状态、受力情况等均发生变化,因此在考试外力做功时,可以分段考虑,也可视全过程为一个过程;两个状态是指初末两个状态的动能。④ 动能定理只对惯性参考系成立,表达式中每一物体的速度都应相对于同一参考系,这个参考系一般是地球.⑤ 动能定理解题,由于它不涉及运动过程中的加速度、时间和中间状态的速度,一般比应用牛顿第二定律结合运动学公式解题要简便且应用范围更广,即可解直线运动,又可解曲线运动即能解匀变...