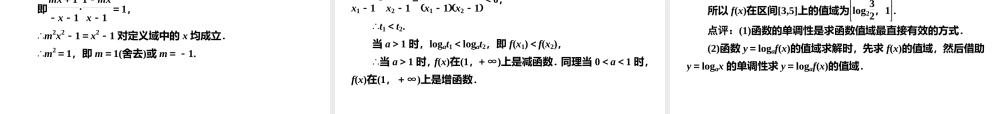第19课时对数函数及其性质的应用目标导航 1.了解指数函数 y=ax(a>0,且 a≠1)与对数函数 y=logax(a>0,且 a≠1)互为反函数.(易混点) 2.理解并掌握对数函数的性质.(重点、难点) 1 新知识·预习探究 知识点 反函数 阅读教材 P73 的有关内容,完成下列问题. (1)对数函数 y=logax(a>0,且 a≠1)的反函数是 y=ax(a>0,且 a≠1). (2)指数函数 y=ax(a>0,且 a≠1)的反函数是 y=logax(a>0,且 a≠1). 【练习】 (1)y=10x 的反函数是__________. (2)y=45x 的反函数是__________. (3)y=log 13x 的反函数是__________. (4)y=log2x 的反函数是__________ 答案:(1)y=lgx (2)y=log 45x (3)y=13x (4)y=2x 2 新视点·名师博客 1.对数函数与指数函数的关系 对数函数 y=logax(a>0,且 a≠1)与 y=ax互为反函数,它们的图象关于直线 y=x 对称.对数函数 y=logax 的定义域是指数函数y=ax 的值域,而 y=logax 的值域是 y=ax 的定义域. 2.比较对数值大小的方法 3.解对数不等式的一般思路 3 新课堂·互动探究 考点一 对数函数与指数函数的关系 例 1 当 0
1,因此 y=a-x=(a-1)x 为增函数且过(0,1),y=logax 为减函数且过(1,0),显然只有 C 符合. 答案:C 点评:解决这类题型的办法有直接法与排除法.直接法一般借助函数的定义域、奇偶性、单调性、过定点等特征对函数的图象进行分析进而得解的方法.排除法通常是利用函数的定义域以及图象经过的一些特殊点进行验证的方法. 变式探究 1 已知 a>0 且 a≠1,函数 y=ax 与 y=loga(-x)的图象只能是图中的( ) A B C D 解析:y=loga(-x)只可能在左半平面,故排除 A,C.再看单调性,y=ax 的单调性与 y=loga(-x)的单调性正好相反,又排除D. 答案:B 考点二 比较对数值的大小 例 2 比较下列各组数的大小: (1)log2π 与 log20.9; (2)log20.3 与 log0.20.3; (3)log0.76,0.76与 60.7; (4)log20.4,log30.4. 分析:观察各组数的特征,利用对数单调性比较大小. 解析:(1)因为函数 y=log2x 在(0,+∞)上是增函数,π>0.9,所以 log2π>log20.9. (2)由...