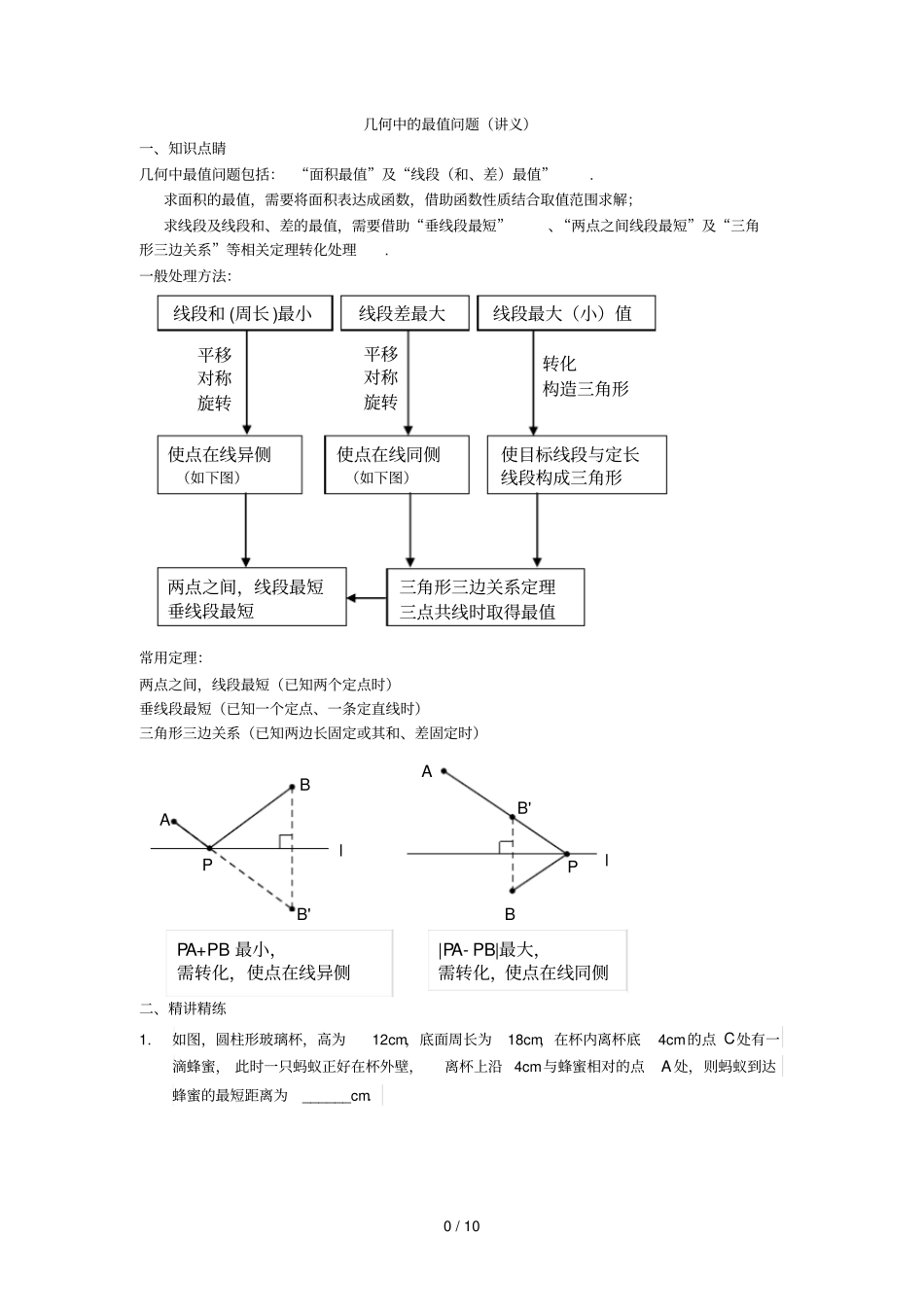
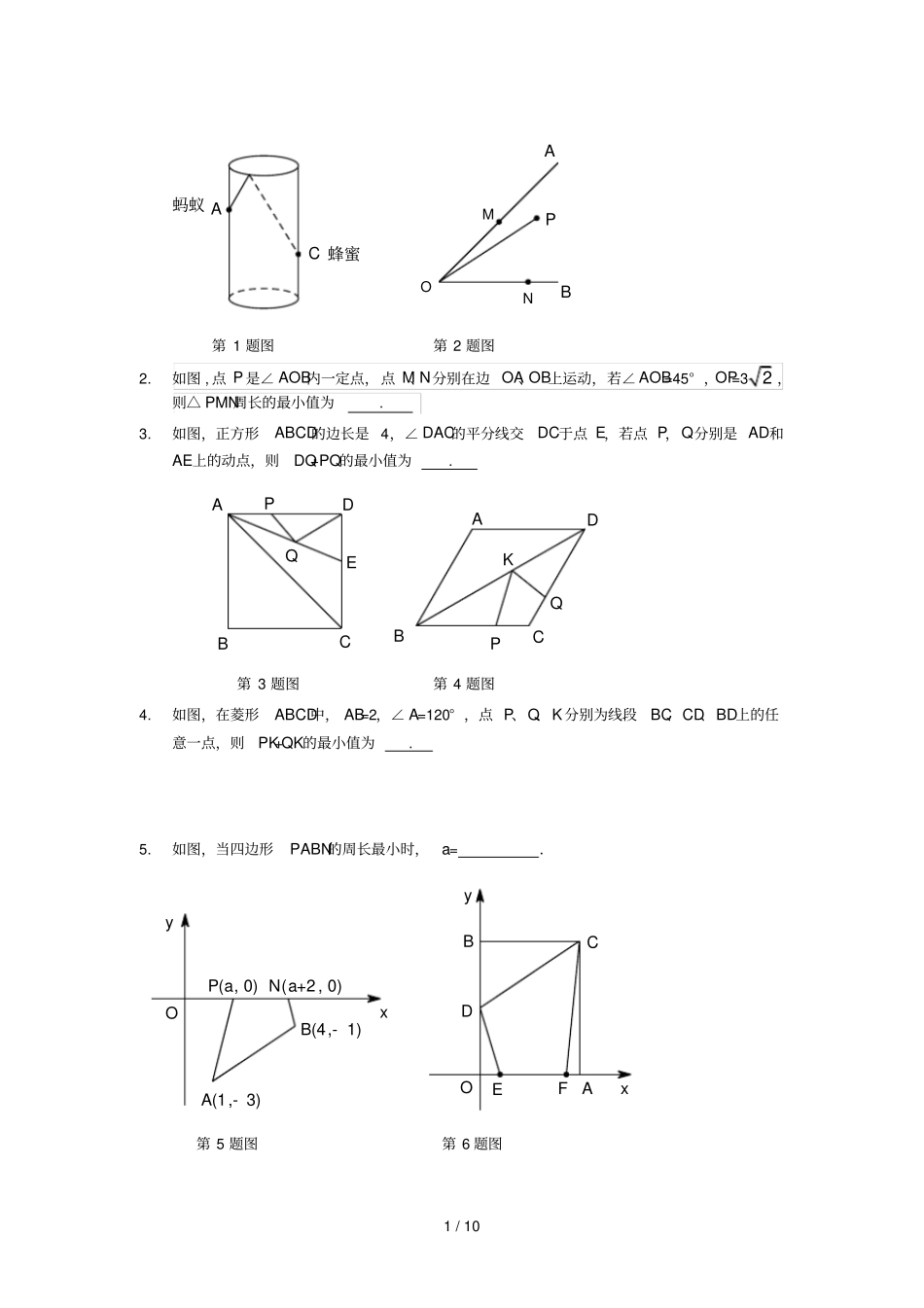
0 / 10 几何中的最值问题(讲义)一、知识点睛几何中最值问题包括: “面积最值”及“线段(和、差)最值”. 求面积的最值,需要将面积表达成函数,借助函数性质结合取值范围求解;求线段及线段和、差的最值,需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理. 一般处理方法:常用定理:两点之间,线段最短(已知两个定点时)垂线段最短(已知一个定点、一条定直线时)三角形三边关系(已知两边长固定或其和、差固定时)lB'BAPlB'ABP二、精讲精练1.如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm的点 C处有一滴蜂蜜, 此时一只蚂蚁正好在杯外壁,离杯上沿 4cm与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为______cm.线段和 (周长 )最小转化构造三角形两点之间,线段最短垂线段最短PA+PB 最小,需转化,使点在线异侧|PA- PB|最大,需转化,使点在线同侧线段差最大线段最大(小)值三角形三边关系定理三点共线时取得最值平移对称旋转使点在线异侧(如下图)使点在线同侧(如下图)使目标线段与定长线段构成三角形平移对称旋转1 / 10 蜂蜜蚂蚁 ACNMOPBA第 1 题图第 2 题图2.如图 , 点 P 是∠ AOB内一定点,点 M、N分别在边 OA、OB上运动,若∠ AOB=45° ,OP=32 ,则△ PMN周长的最小值为 . 3.如图,正方形ABCD的边长是 4,∠ DAC的平分线交DC于点 E,若点 P,Q分别是 AD和AE上的动点,则DQ+PQ的最小值为 . QPEDCBAQPKDCBA第 3 题图第 4 题图4.如图,在菱形ABCD中, AB=2,∠ A=120° ,点 P、Q、K 分别为线段BC、CD、BD上的任意一点,则PK+QK的最小值为 . 5.如图,当四边形PABN的周长最小时,a= .N(a+2 , 0)P(a, 0)B(4,- 1)A(1,- 3)OyxFDCBAxyOE第 5 题图第 6 题图2 / 10 6.在平面直角坐标系中,矩形OACB的顶点 O在坐标原点,顶点A、B 分别在 x 轴、y 轴的正半轴上, OA=3,OB=4,D为边 OB的中点 . 若 E、F 为边 OA上的两个动点,且EF=2,当四边形 CDEF的周长最小时,则点F 的坐标为 . 7.如图,两点 A、B 在直线 MN外的同侧, A 到 MN的距离 AC=8,B 到 MN的距离 BD=5,CD=4,P在直线 MN上运动,则PAPB 的最大值等于.ABCDPMNxOABy第 7 题图第 8 题图8.点 A、B 均在由面积为1 的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若 P 是 x 轴上使得PAPB 的值最大...