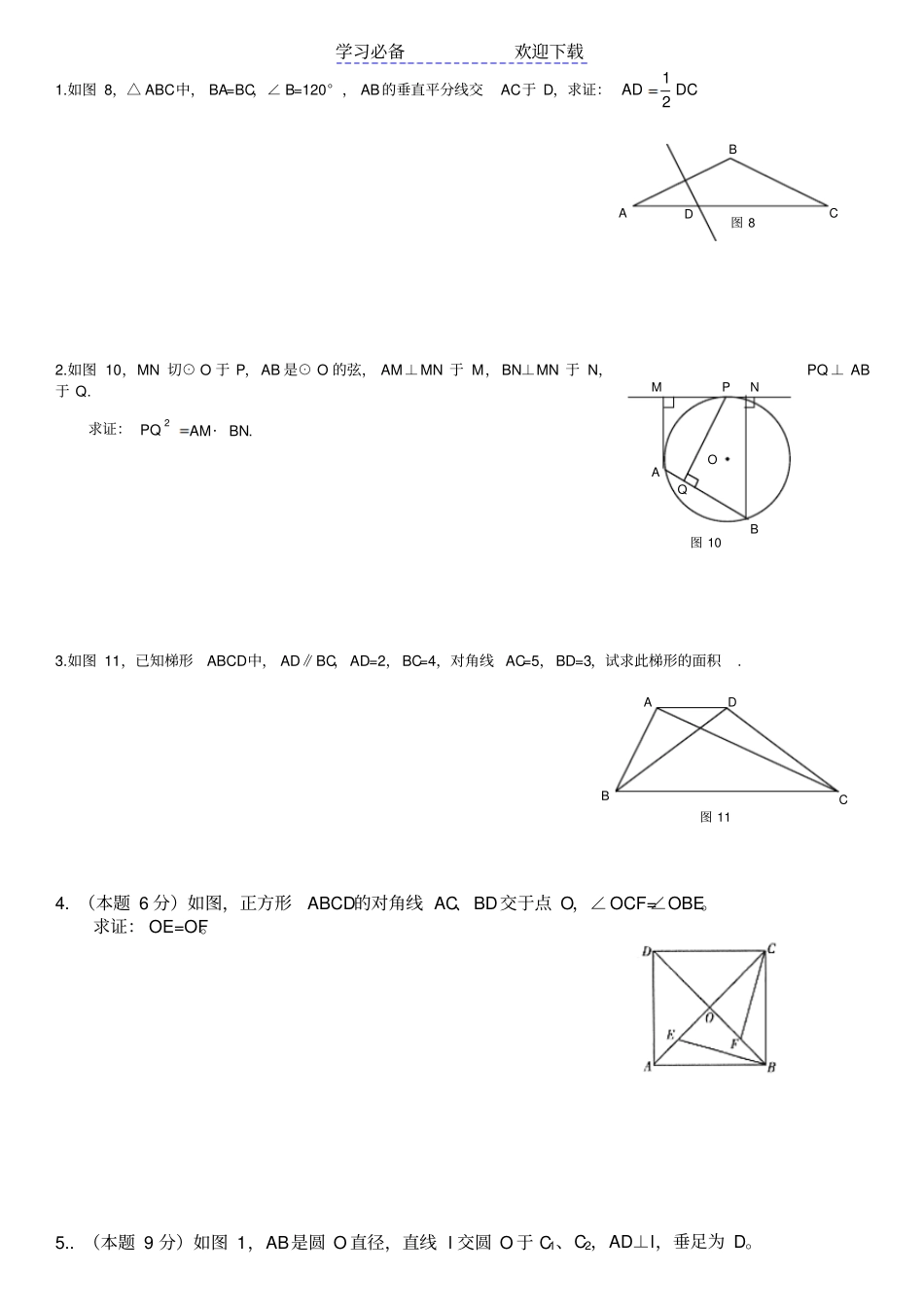
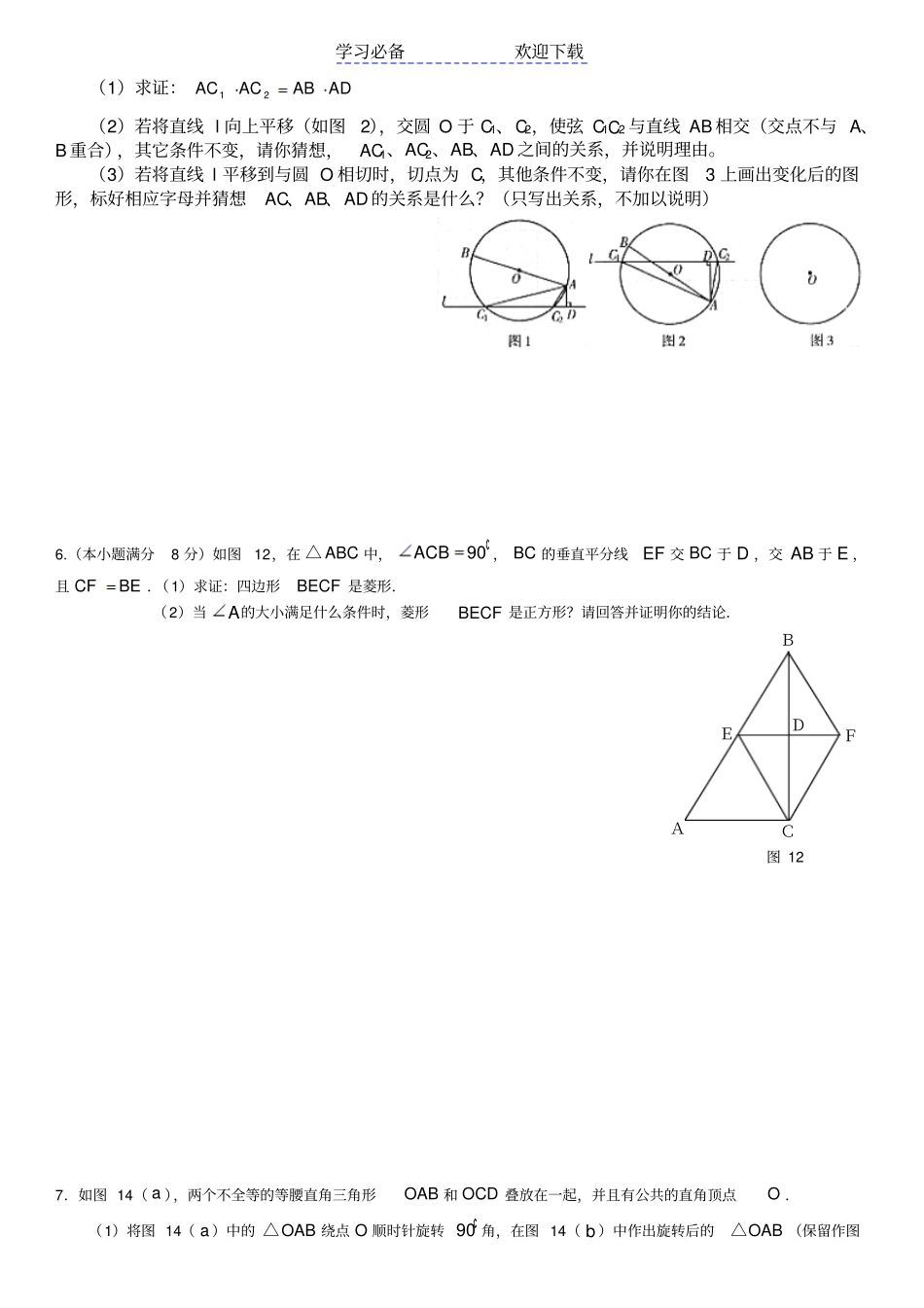
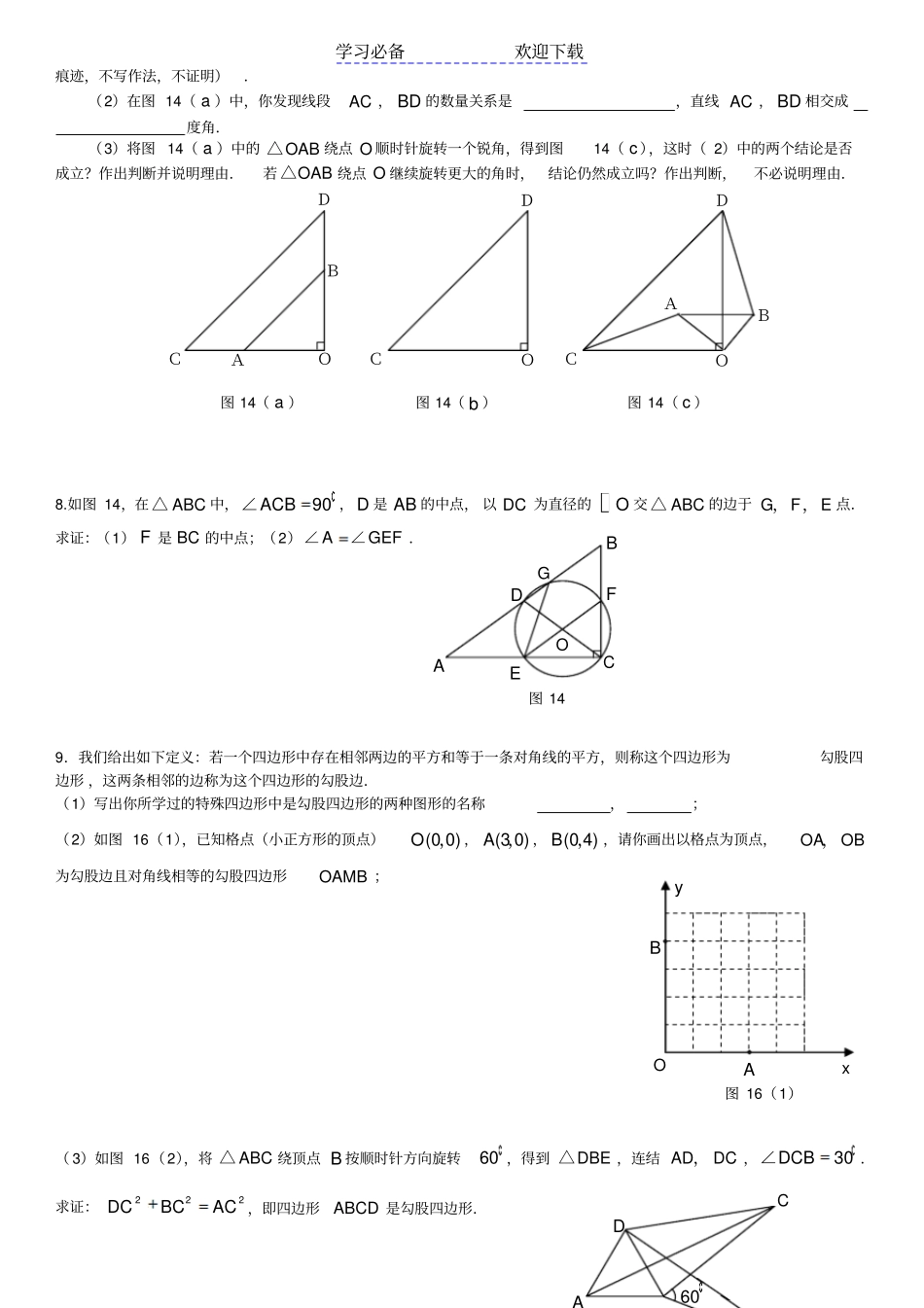
学习必备欢迎下载1.如图 8,△ ABC中, BA=BC,∠ B=120° , AB的垂直平分线交AC于 D,求证:DCAD212.如图 10,MN 切⊙ O 于 P,AB 是⊙ O 的弦, AM⊥MN 于 M,BN⊥MN 于 N,PQ ⊥ AB于 Q. 求证:2PQAM·BN. 3.如图 11,已知梯形ABCD中, AD∥BC,AD=2,BC=4,对角线 AC=5,BD=3,试求此梯形的面积. 4. (本题 6 分)如图,正方形ABCD的对角线 AC、BD交于点 O,∠ OCF=∠OBE。求证: OE=OF。5.. (本题 9 分)如图 1,AB是圆 O 直径,直线 l 交圆 O 于 C1、C2,AD⊥l,垂足为 D。B A C D 图 8 M N P Q O A B 图 10 A B C D 图 11 学习必备欢迎下载(1)求证:ADABACAC21(2)若将直线 l 向上平移(如图2),交圆 O 于 C1、C2,使弦 C1C2 与直线 AB 相交(交点不与 A、B 重合),其它条件不变,请你猜想,AC1、AC2、AB、AD 之间的关系,并说明理由。(3)若将直线 l 平移到与圆 O 相切时,切点为 C,其他条件不变,请你在图3 上画出变化后的图形,标好相应字母并猜想AC、AB、AD 的关系是什么?(只写出关系,不加以说明)6.(本小题满分8 分)如图12,在ABC△中,90ACB, BC 的垂直平分线EF 交 BC 于 D ,交 AB 于 E ,且 CFBE .(1)求证:四边形BECF 是菱形.(2)当A的大小满足什么条件时,菱形BECF 是正方形?请回答并证明你的结论.7.如图 14( a ),两个不全等的等腰直角三角形OAB 和 OCD 叠放在一起,并且有公共的直角顶点O .(1)将图 14( a )中的OAB△绕点 O 顺时针旋转 90 角,在图 14( b )中作出旋转后的OAB△(保留作图BFCAED图 12 学习必备欢迎下载痕迹,不写作法,不证明).(2)在图 14( a )中,你发现线段AC , BD 的数量关系是,直线 AC , BD 相交成度角.(3)将图 14( a )中的OAB△绕点 O 顺时针旋转一个锐角,得到图14( c ),这时( 2)中的两个结论是否成立?作出判断并说明理由.若OAB△绕点 O 继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.8.如图 14,在ABC△中,90ACB∠, D 是 AB 的中点, 以 DC 为直径的O 交ABC△的边于 GFE,,点.求证:(1) F 是 BC 的中点;(2)AGEF∠∠.9.我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形 ,这两条相邻的...