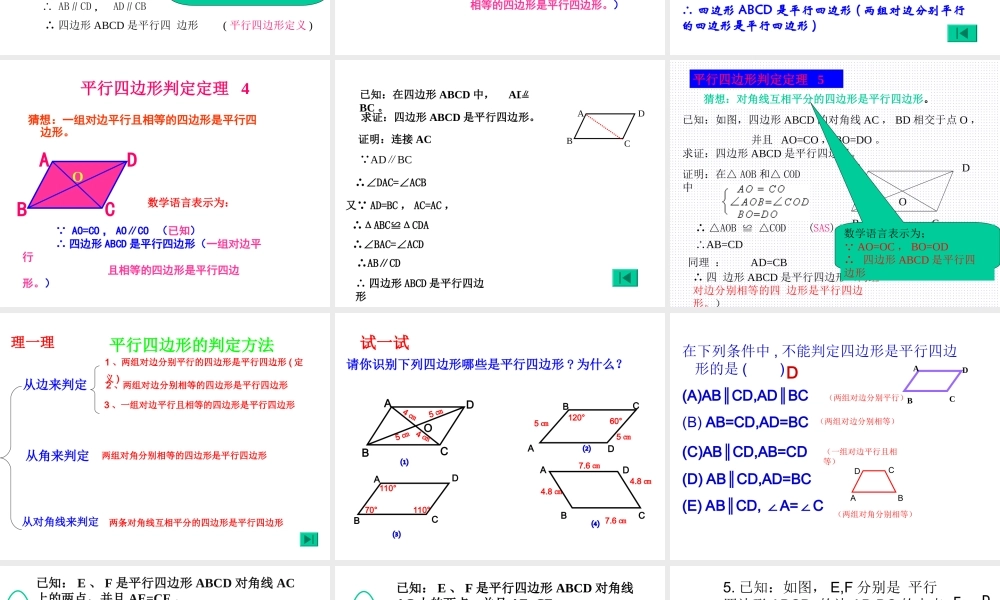
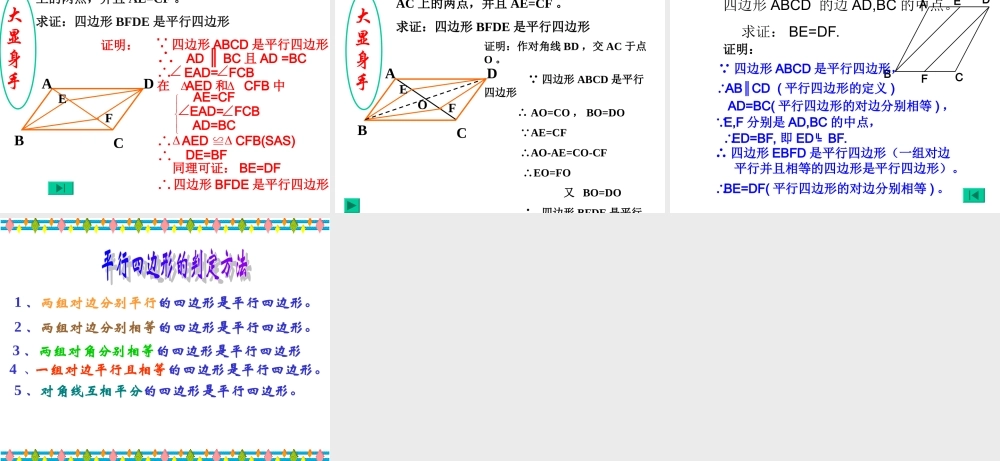
边平行四边形的对边平行且相等角对角线 平行四边形的对角线互相平分平行四边形的性质:BDACO 四边形 ABCD 是平行四边形 ∴ AB CD , AD BC∥ ﹦ ∥ ﹦ 平行四边形的对角相等,邻角互补 四边形 ABCD 是平行边形 ∴ ∠ A= ∠ C , ∠ D=∠ B ∠ A+∠ B= , ∠ A+∠ D= …01800180 四边形 ABCD 是平行边形 ∴ OA=OC,OB=OD 平行四边形判定定理 1• 1. 两组对边分别平行的四边形是平行四边形。ABCD AB∥CD , AD∥BC (已知) ∴ 四边形 ABCD 是平行四边形(两组对 边分别平行的四边形是平 行四边形。) 数学语言表示为: 学习了平行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。 小辉却问:你凭什么确定这四边形就是平行四边形呢? 大家都困惑了…… 猜想:两组对边分别相等的四 边形是平行四边形。 已知:如图,在四边形 ABCD 中, AD=CB , AB=CD求证:四边形 ABCD 是平行四边形。证明:连结 AC∴ABC ≌△ CDA (SSS) ∴∠1=2∠ ,∠ 3=4∠1234∴ AB∥CD , AD∥CB∴ 四边形 ABCD 是平行四 边形 ( 平行四边形定义 )判定定理 2 :数学语言表示为: AD=CB , AB=CD∴ 四边形 ABCD 是平行四 边形 平行四边形判定定理 3猜想:两组对角分别相等的四边形是平行四边形。ABCD ∠A= ∠C , ∠ B= ∠D (已知) ∴ 四边形 ABCD 是平行四边形(两组对角分别 相等的四边形是平行四边形。)数学语言表示为: BDAC已知:四边形 ABCD, ∠A=∠C∠,B=∠D求证:四边形 ABCD 是平行四边形证明:∴ 四边形 ABCD 是平行四边形 ( 两组对边分别平行的四边形是平行四边形 )同理可证 AB∥CD又 ∠ A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 ° ∠A=∠C ,∠ B=∠D (已知)即∠ A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行) 平行四边形判定定理 4猜想:一组对边平行且相等的四边形是平行四边形。ABCD AO=CO , AO∥CO (已知) ∴ 四边形 ABCD 是平行四边形(一组对边平行 且相等的四边形是平行四边形。)O数学语言表示为: ABCD求证:四边形 ABCD 是平行四边形。 证明:连接 AC AD∥BC ∴∠DAC=∠ACB又 AD=BC , AC=AC , ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴ 四边形 ABCD 是平行四边形 已知:在四边形 ABCD...