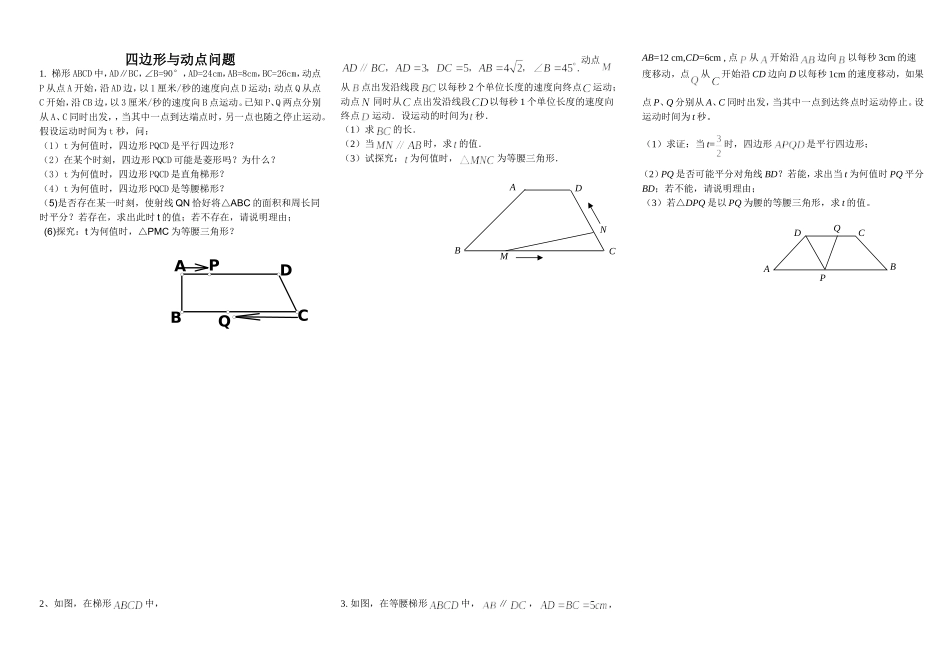
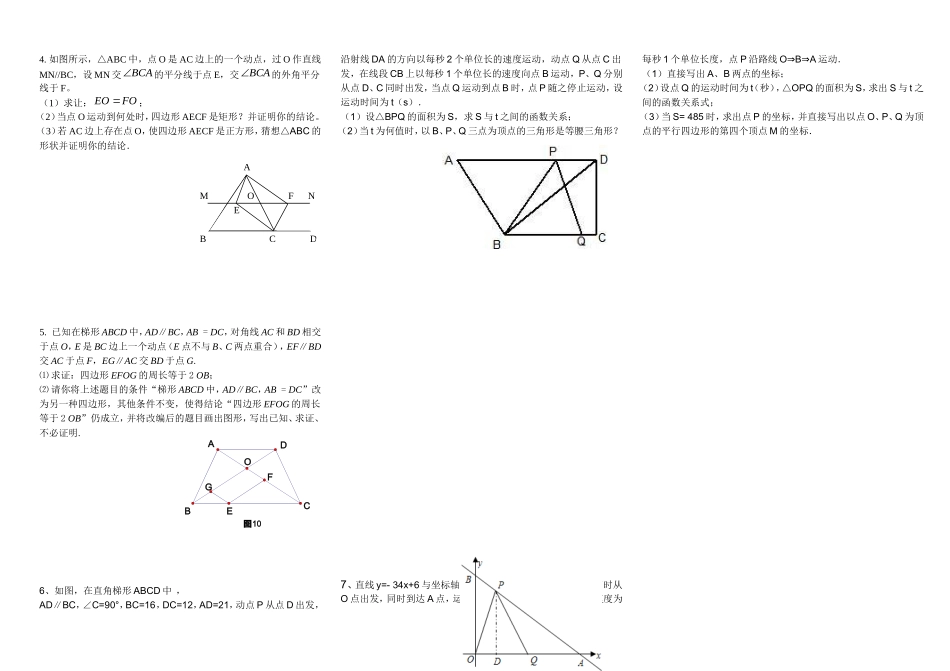
四边形与动点问题1. 梯形 ABCD 中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P 从点 A 开始,沿 AD 边,以 1 厘米/秒的速度向点 D 运动;动点 Q 从点C 开始,沿 CB 边,以 3 厘米/秒的速度向 B 点运动。已知 P、Q 两点分别从 A、C 同时出发,,当其中一点到达端点时,另一点也随之停止运动。假设运动时间为 t 秒,问:(1)t 为何值时,四边形 PQCD 是平行四边形?(2)在某个时刻,四边形 PQCD 可能是菱形吗?为什么?(3)t 为何值时,四边形 PQCD 是直角梯形?(4)t 为何值时,四边形 PQCD 是等腰梯形?(5)是否存在某一时刻,使射线 QN 恰好将△ABC 的面积和周长同时平分?若存在,求出此时 t 的值;若不存在,请说明理由;(6)探究:t 为何值时,△PMC 为等腰三角形?2、如图,在梯形中,动点从点出发沿线段以每秒 2 个单位长度的速度向终点运动;动点同时从点出发沿线段以每秒 1 个单位长度的速度向终点运动.设运动的时间为 秒.(1)求的长.(2)当时,求 的值.(3)试探究: 为何值时,为等腰三角形. 3. 如图,在等腰梯形中,∥,,AB=12 cm,CD=6cm , 点从开始沿边向以每秒 3cm 的速度移动,点从开始沿 CD 边向 D 以每秒 1cm 的速度移动,如果点 P、Q 分别从 A、C 同时出发,当其中一点到达终点时运动停止。设运动时间为 t 秒。(1)求证:当 t=时,四边形是平行四边形;(2)PQ 是否可能平分对角线 BD?若能,求出当 t 为何值时 PQ 平分BD;若不能,请说明理由;(3)若△DPQ 是以 PQ 为腰的等腰三角形,求 t 的值。ADCBMNABCDPQABCDQP A M O F N E B C D 4. 如图所示,△ABC 中,点 O 是 AC 边上的一个动点,过 O 作直线MN//BC,设 MN 交BCA 的平分线于点 E,交BCA 的外角平分线于 F。(1)求让: EOFO;(2)当点 O 运动到何处时,四边形 AECF 是矩形?并证明你的结论。(3)若 AC 边上存在点 O,使四边形 AECF 是正方形,猜想△ABC 的形状并证明你的结论.5. 已知在梯形 ABCD 中,AD∥BC,AB = DC,对角线 AC 和 BD 相交于点 O,E 是 BC 边上一个动点(E 点不与 B、C 两点重合),EF∥BD交 AC 于点 F,EG∥AC 交 BD 于点 G.⑴ 求证:四边形 EFOG 的周长等于 2 OB;⑵ 请你将上述题目的条件“梯形 ABCD 中,AD∥BC,AB = DC”改为另一种四边形,其他条件...