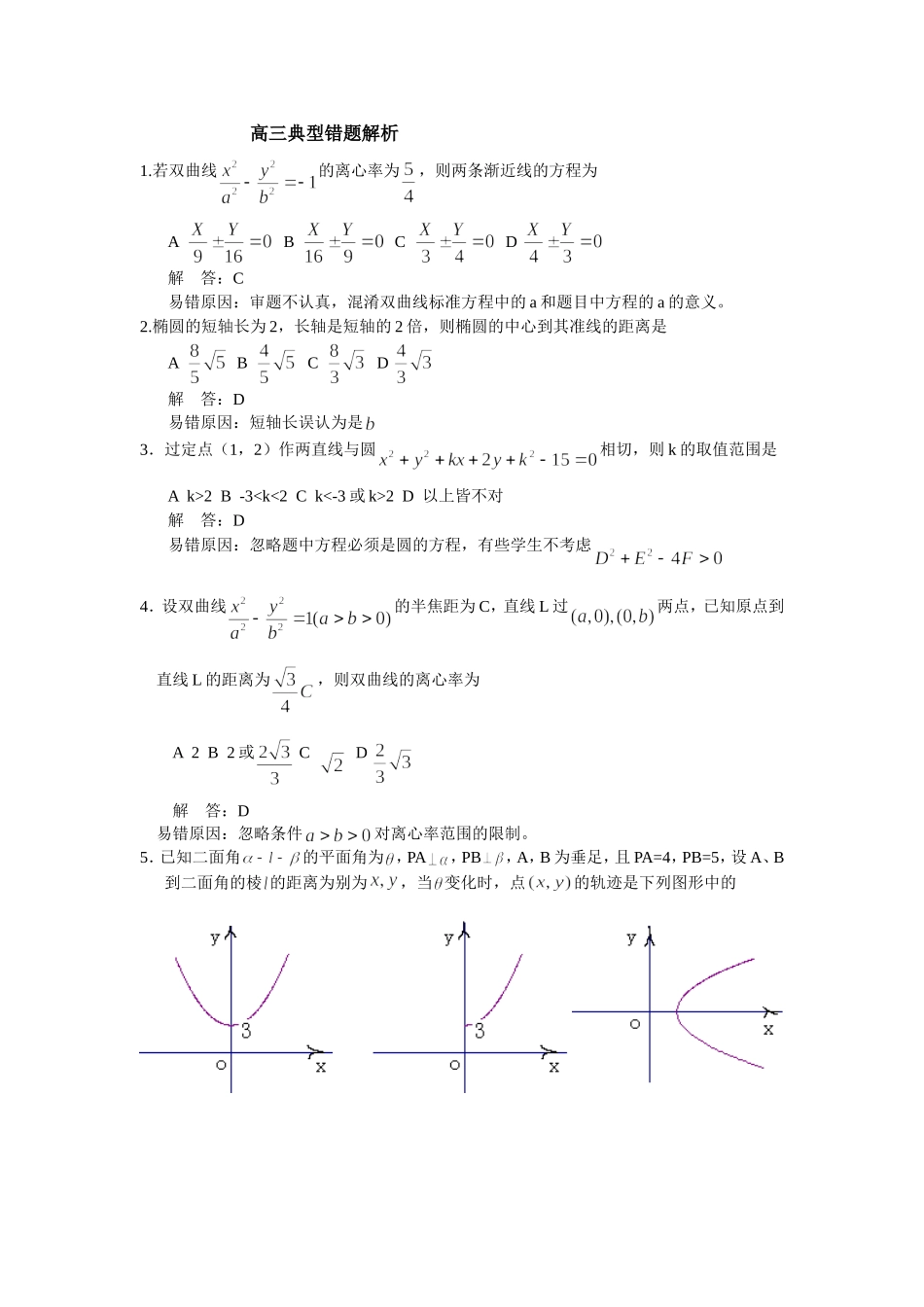
高三典型错题解析1.若双曲线的离心率为,则两条渐近线的方程为A B C D 解 答:C易错原因:审题不认真,混淆双曲线标准方程中的 a 和题目中方程的 a 的意义。2.椭圆的短轴长为 2,长轴是短轴的 2 倍,则椭圆的中心到其准线的距离是A B C D 解 答:D易错原因:短轴长误认为是3.过定点(1,2)作两直线与圆相切,则 k 的取值范围是A k>2 B -32 D 以上皆不对解 答:D易错原因:忽略题中方程必须是圆的方程,有些学生不考虑4.设双曲线的半焦距为 C,直线 L 过两点,已知原点到直线 L 的距离为,则双曲线的离心率为A 2 B 2 或 C D 解 答:D 易错原因:忽略条件对离心率范围的限制。5.已知二面角的平面角为 ,PA,PB,A,B 为垂足,且 PA=4,PB=5,设 A、B到二面角的棱 的距离为别为,当 变化时,点的轨迹是下列图形中的 A B C D解 答: D 易错原因:只注意寻找的关系式,而未考虑实际问题中的范围。6.(如中)若曲线与直线+3 有两个不同的公共点,则实数 k 的取值范围是A B C D 解 答:C 易错原因:将曲线转化为时不考虑纵坐标的范围;另外没有看清过点(2,-3)且与渐近线平行的直线与双曲线的位置关系。7.(石庄中学)P(-2,-2)、Q(0,-1)取一点 R(2,m)使︱PR︱+︱RQ︱最小,则 m=( )A B 0 C –1 D -正确答案:D 错因:学生不能应用数形结合的思想方法,借助对称来解题。8.(石庄中学)能够使得圆 x +y -2x+4y+1=0 上恰好有两个点到直线 2x+y+c=0 距离等于 1 的一个值为( )A 2 B C 3 D 3 正确答案: C 错因:学生不能借助圆心到直线的距离来处理本题。9.(石庄中学)P (x ,y )是直线 L:f(x,y)=0 上的点,P (x ,y )是直线 L 外一点,则方程 f(x,y)+f(x ,y )+f(x ,y )=0 所表示的直线( )A 相交但不垂直 B 垂直 C 平行 D 重合正确答案: C 错因:学生对该直线的解析式看不懂。10.(石庄中学)已知圆+y =4 和 直线 y=mx 的交点分别为 P、Q 两点,O 为坐标原点, 则︱OP︱·︱OQ︱=( )A 1+m B C 5 D 10正确答案: C 错因:学生不能结合初中学过的切割线定︱OP︱·︱OQ︱等于切线长的平方来解题。11.(石庄中学)在圆 x +y =5x 内过点(, )有 n 条弦的长度成等差数列,最短弦长为数列首项 a ,最长弦长为 a ,若公差 d,那么 n 的取值集合为( )A B C D 正确...