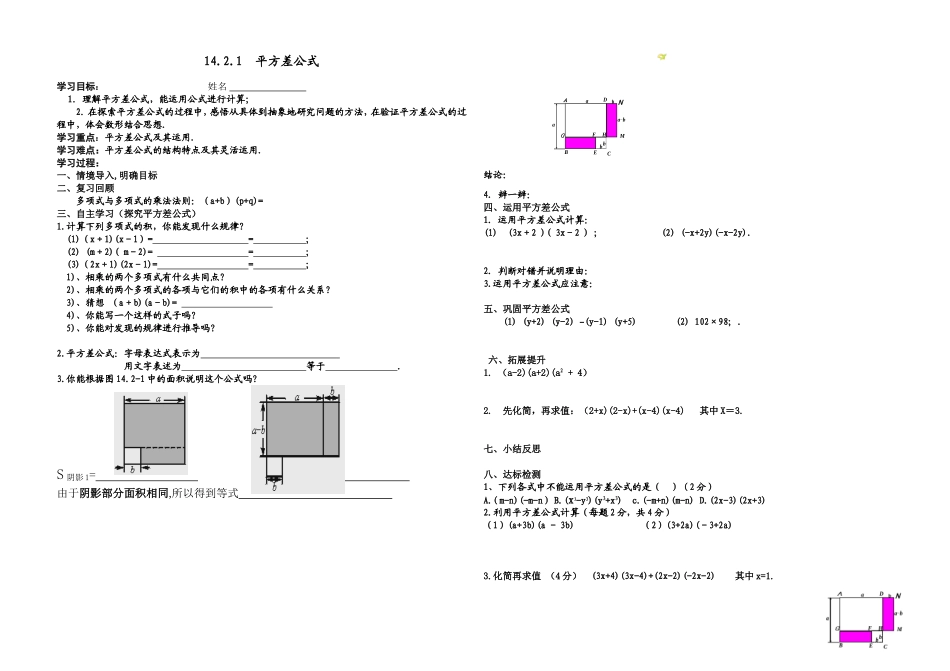
14.2.1 平方差公式 学习目标: 姓名 1.理解平方差公式,能运用公式进行计算; 2.在探索平方差公式的过程中,感悟从具体到抽象地研究问题的方法,在验证平方差公式的过程中,体会数形结合思想.学习重点:平方差公式及其运用.学习难点:平方差公式的结构特点及其灵活运用.学习过程:一、情境导入,明确目标二、复习回顾 多项式与多项式的乘法法则:(a+b)(p+q)=三、自主学习(探究平方差公式)1.计算下列多项式的积,你能发现什么规律?(1)(x+1)(x-1)= = ; (2) (m+2)( m-2)= = ; (3)(2x+1)(2x-1)= = ; 1)、相乘的两个多项式有什么共同点? 2)、相乘的两个多项式的各项与它们的积中的各项有什么关系? 3)、猜想 (a+b)(a-b)= 4)、你能写一个这样的式子吗? 5)、你能对发现的规律进行推导吗? 2.平方差公式:字母表达式表示为 用文字表述为 等于 . 3.你能根据图 14.2-1 中的面积说明这个公式吗? 图 1 图 2S 阴影 1= S 阴影 2= 由于阴影部分面积相同,所以得到等式 结论:AMBCDEHaabba-bbFGN4. 辨一辨:四、运用平方差公式1. 运用平方差公式计算:(1) (3x+2 )( 3x-2 ) ; (2) (-x+2y)(-x-2y).2. 判断对错并说明理由:3.运用平方差公式应注意:五、巩固平方差公式 (1) (y+2) (y-2) (y-1) (y+5) – (2) 102×98; . 六、拓展提升 1. (a-2)(a+2)(a2 + 4) 2. 先化简,再求值:(2+x)(2-x)+(x-4)(x-4) 其中 X=3.七、小结反思八、达标检测1、下列各式中不能运用平方差公式的是( )(2 分)A.(m-n)(-m-n) B.(x3-y3)(y3+x3) c.(-m+n)(m-n) D.(2x-3)(2x+3)2.利用平方差公式计算(每题 2 分,共 4 分)(1)(a+3b)(a - 3b) (2)(3+2a)(-3+2a) 3.化简再求值 (4 分) (3x+4)(3x-4)+(2x-2)(-2x-2) 其中 x=1.