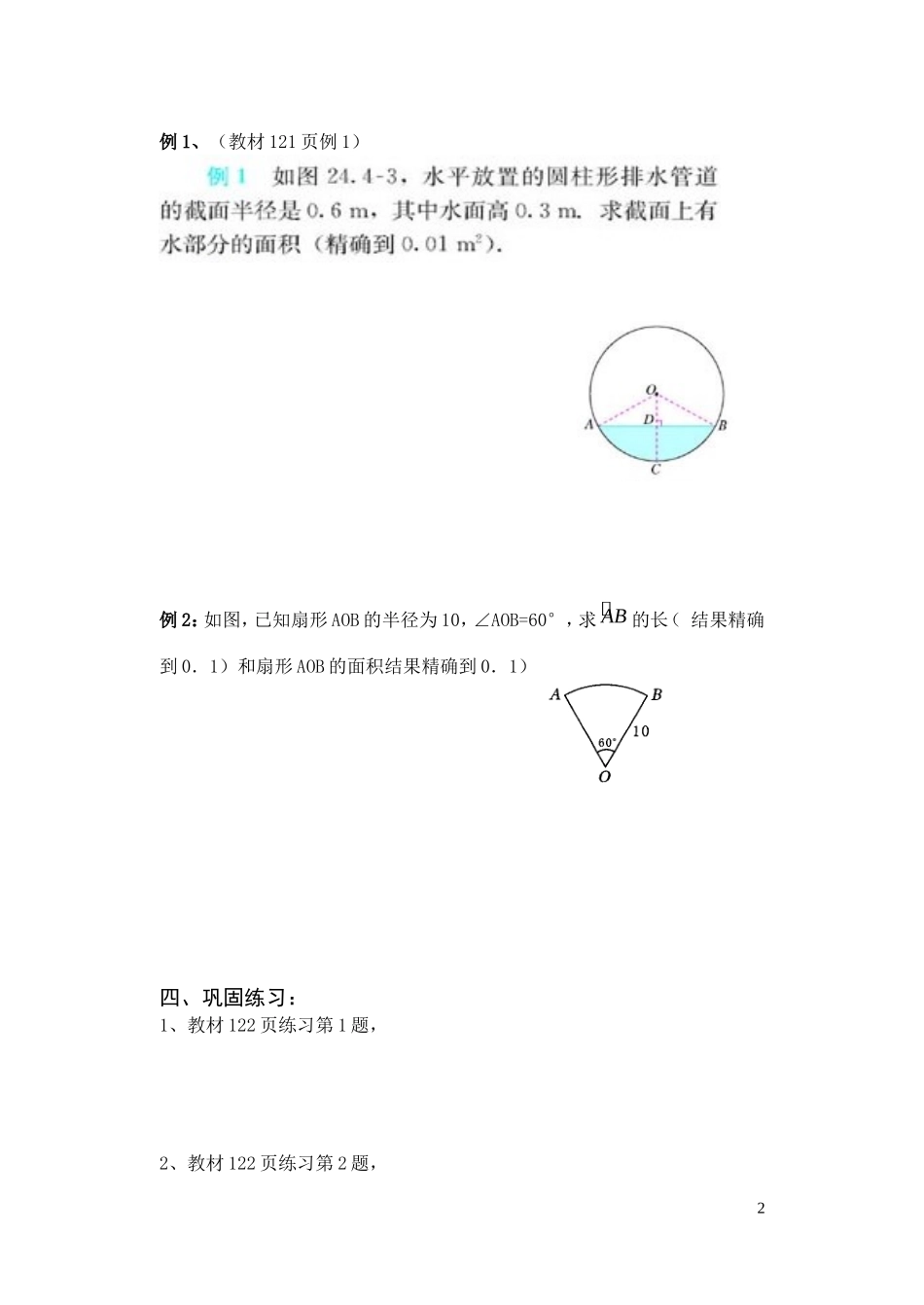
24.4 弧长和扇形面积(第 1 课时)【学习目标】1、 了解扇形的概念,理解 n ° 的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用.2、 通过复习圆的周长、圆的面积公式,探索 n°的圆心角所对的弧长 L=和扇形面积 S 扇=的计算公式,并应用这些公式解决一些题目.【学习过程】一、温故知新:1.圆的周长公式是 。2.圆的面积公式是 。3.什么叫弧长?二、自主学习:自学教材 P120----P121,思考下列内容:1、圆的周长可以看作______度的圆心角所对的弧. 1°的圆心角所对的弧长是_______。 2°的圆心角所对的弧长是_______。 4°的圆心角所对的弧长是_______。 …… n°的圆心角所对的弧长是_______。2、什么叫扇形?3、圆的面积可以看作 度圆心角所对的扇形的面积; 设圆的半径为 R,1°的圆心角所对的扇形面积 S 扇形=_______。 设圆的半径为 R,2°的圆心角所对的扇形面积 S 扇形=_______。 设圆的半径为 R,5°的圆心角所对的扇形面积 S 扇形=_______。 …… 设圆的半径为 R,n°的圆心角所对的扇形面积 S 扇形=_______。4、比较扇形面积公式和弧长公式,如何用弧长表示扇形的面积?三、典型例题:1例 1、(教材 121 页例 1) 例 2:如图,已知扇形 AOB 的半径为 10,∠AOB=60°,求 AB 的长(结果精确到 0.1)和扇形 AOB 的面积结果精确到 0.1) 四、巩固练习:1、教材 122 页练习第 1 题,2、教材 122 页练习第 2 题, 23、习题 24.4 第 1 题填空。(答案写在教材上)五、总结反思:【达标检测】1、已知扇形的圆心角为 120°,半径为 6,则扇形的弧长是( ). A.3 B.4 C.5 D.62、如图所示,把边长为 2 的正方形 ABCD 的一边放在定直线 L 上,按顺时针方向绕点 D 旋转到如图的位置,则点 B 运动到点 B′所经过的路线长度为( )A.1 B. C.2 D.2 BAC(A')DlB'C' (第 2 题图) (第 3 题图) (第 4 题图)3、如图所示,OA=30B,则 AD 的长是 BC 的长的_____倍.4、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中为,长为 8cm,长为 12cm,则阴影部分的面积为 。5、(2008 常州)已知扇形的半径为 3cm,扇形的弧长为 πcm,则该扇形的面积是______cm2,扇形的圆心角为______°.6、(2007 山东济宁)如图,从 P 点引⊙O 的两切线 PA、PA、PB,A、B 为切点,已知⊙ O ...