2014年新人教A版数学必修二421《直线与圆的位置关系》课件VIP免费

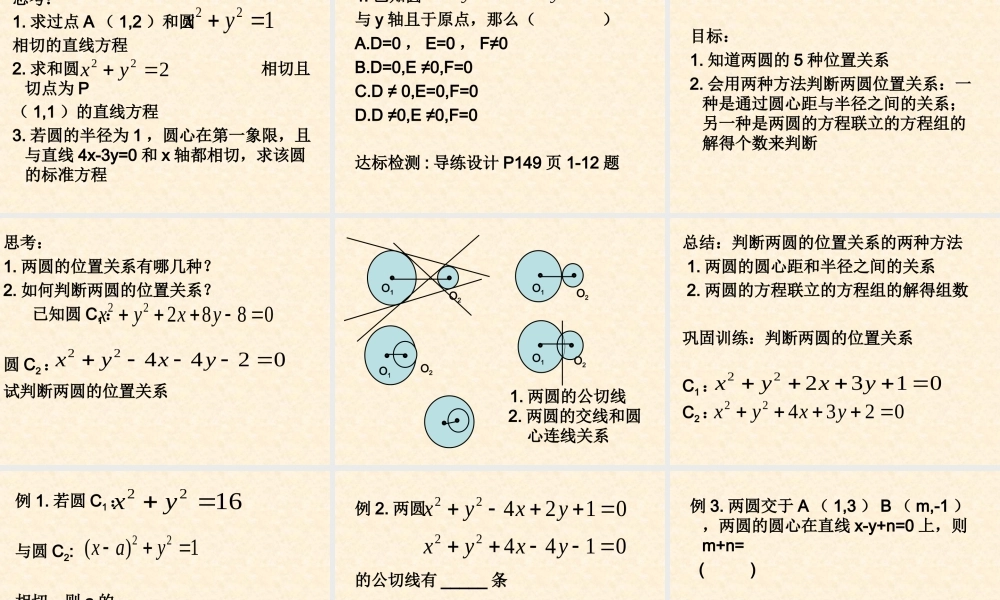
2 直线､圆的位置关系 4

1 直线与圆的位置关系 1

了解直线与圆的位置关系 , 有相离､相切､相交三种情形

会用几何法 (d 与 r 的关系 ) ､代数法 ( 直线方程与圆的方程解的组数 ) 来判断直线与圆的位置关系

问题：一个小岛的周围有环形暗礁，暗礁分布在以小岛的中心为圆心，半径为 30km 的圆形区域

小岛中心位于轮船正西 70km 处，港口位于小岛中心正北 40km 处，如果轮船沿直线返航，它是否有触礁危险

O港口轮船直线与圆有三种位置关系 : (1) 直线与圆 ________, 有两个公共点

(2) 直线与圆 ________, 有一个公共点

(3) 直线与圆 ________, 没有公共点

相交相切相离思考：如何判断直线和圆的位置关系

结合刚说的问题 1

判断直线与圆的位置关系的两种方法(1) 利用圆心到直线的距离 d 与半径 r 的大小判断 :dr⇔相离

(2) 联立直线与圆的方程组成方程组 , ，判断方程组有没有解

已知直线 l:3x+y-6=0 和圆心为 C 的圆判断直线和圆的位置关系，如果相交，求它们的交点坐标例 2

已知圆的方程直线 y=x+b, 当 b 为何值时① 圆与直线有两个公共点；② 圆与直线只有一个公共点；③ 圆与直线没有公共点04222yyx自我检测：教材 P128 页 2-4 题，达标检测 : 教材 P132 页 A 组的 1-3题第二课时目标：会解决直线与圆相交的弦长问题例 1

求直线 l:3x-y-6=0 被圆 C ：截得的弦 AB 的长例 2

已知过点 M （ -3 ， -3 ）的直线 l 被圆 截得的弦长为，求直线 l 的方程04222yxyx021422yyx54有关直线与圆相交所得的弦长问题 一般地 , 求直线与圆相交所得的弦长 ,可结合垂径定理