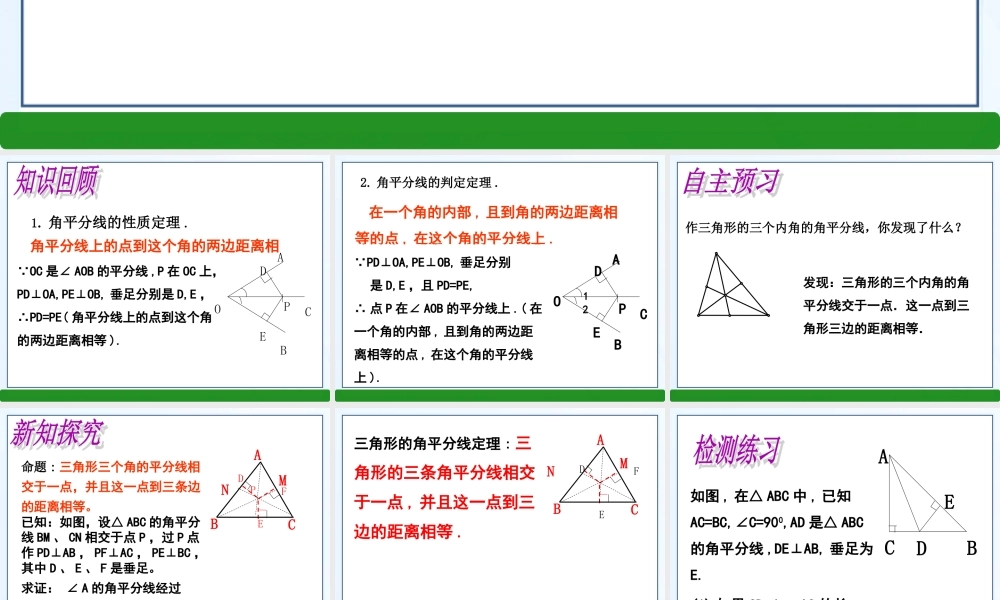
义务教育教科书(北师大版)八年级数学下册第一章 三角形的证明角平分线上的点到这个角的两边距离相等 .∵OC 是∠ AOB 的平分线 ,P 在 OC 上,PD⊥OA,PE⊥OB, 垂足分别是 D,E ,∴PD=PE( 角平分线上的点到这个角的两边距离相等 ).AOCBPDE1. 角平分线的性质定理 . 在一个角的内部 , 且到角的两边距离相等的点 , 在这个角的平分线上 .∵PD⊥OA,PE⊥OB, 垂足分别 是 D,E ,且 PD=PE, ∴ 点 P 在∠ AOB 的平分线上 .( 在一个角的内部 , 且到角的两边距离相等的点 , 在这个角的平分线上 ).AOCB12PDE2. 角平分线的判定定理 .作三角形的三个内角的角平分线,你发现了什么? 发现:三角形的三个内角的角平分线交于一点.这一点到三角形三边的距离相等.命题 : 三角形三个角的平分线相交于一点,并且这一点到三条边的距离相等。已知:如图,设△ ABC 的角平分线 BM 、 CN 相交于点 P ,过 P 点作 PD⊥AB , PF⊥AC , PE⊥BC ,其中 D 、 E 、 F 是垂足。求证: ∠ A 的角平分线经过 点 P ,且 PD=PE=PF .PDEFABCMN三角形的角平分线定理 : 三角形的三条角平分线相交于一点 , 并且这一点到三边的距离相等 .DEFABCMN如图 , 在△ ABC 中 , 已知AC=BC,∠C=900,AD 是△ ABC的角平分线 ,DE⊥AB, 垂足为E.(1) 如果 CD=4cm,AC 的长 ;(2) 求证 :AB=AC+CD.EDABC定 理: 角平分线上的点到这个角的两边距离相等 . 逆定理: 在一个角的内部 , 且到角的两边距离相 等的点 , 在这个角的平分线上 .定 理 : 三角形的三条角平分线相交于一点 , 并且这一点到三边的距离相等 ( 这个交点叫做三角形的内心 ).我今天学到了……你今天这节课有什么收获呢?1.P32 页第 2 题 2. 梳理本章内容,罗列本章知识结构框架图