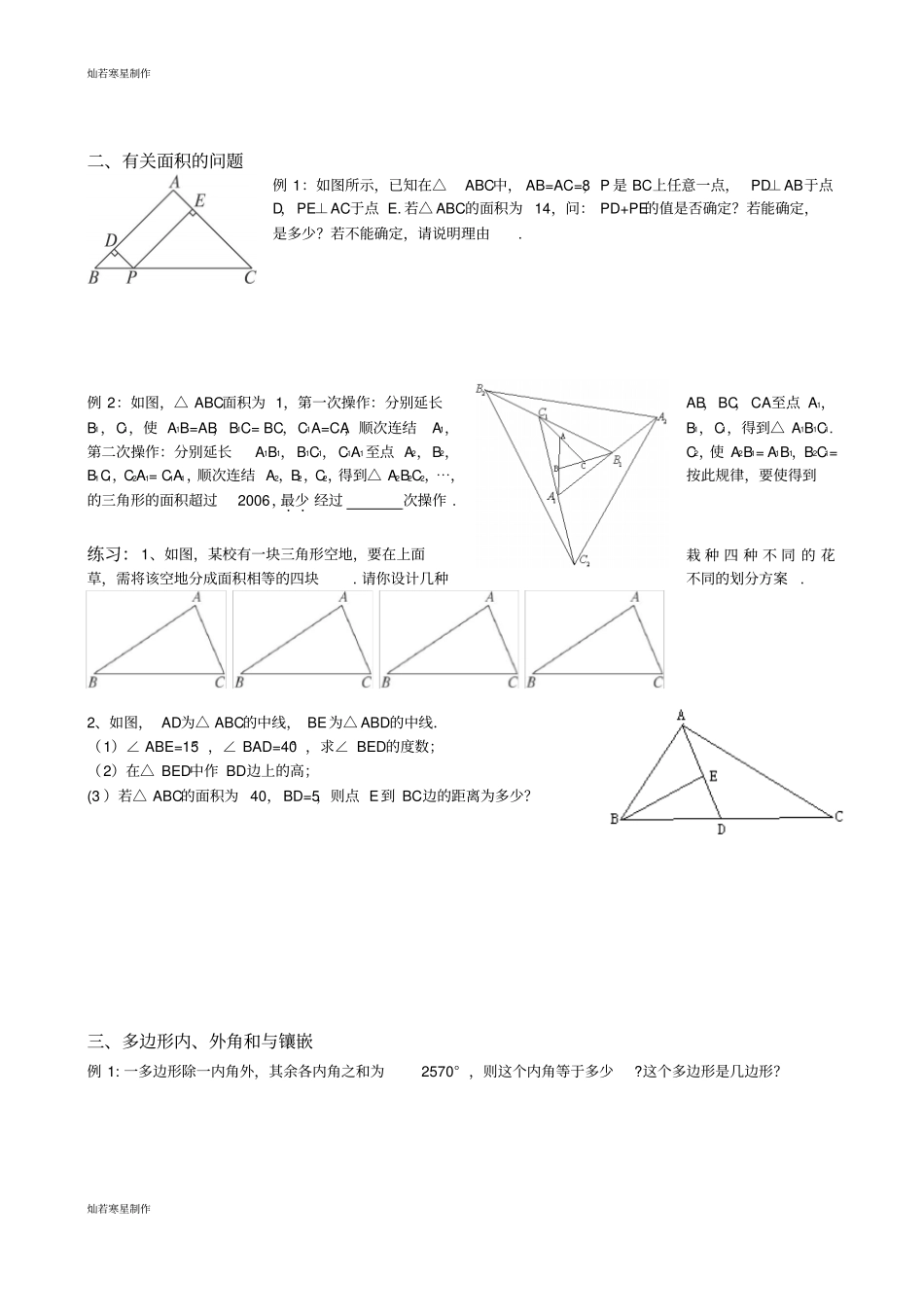
灿若寒星制作灿若寒星制作一、边之间的关系的应用例 1:a,b,c 是三角形的三条边长,化简:|a+b+c| - |a-b-c|-|a-b+ c|- |a+b-c|. 例 2:已知:如图,在△ABC中有 D、E 两点,求证: BD+DE+ EC<AB+AC.例 3:不等边三角形的高分别为4 和 12,若第三条高的长度也是整数,试求它的长。练习: 1:a、 b、c 是△ ABC 的边长,化简 |a-b-c|+|a+b-c|-|-a-b-c| 2:如图,已知P 是△ ABC内任意一点,求证:PB+PC<AB+AC。任意一点,试说明 AB+ BC+CA>PA+PB+PC>21 (AB+BC3:已知 P 是△ ABC内+CA)的理由 . 灿若寒星制作灿若寒星制作4、如图,在△ ABC中, AD是 BC边上的中线,△ADC的周长比△ ABD的周长多 5cm,AB与 AC的和为 11cm,求 AC的长.二、角之间关系的应用例 1:已知非直角三角形ABC中,∠ A=45° ,高 BD和 CE所在的直线交于H,你能求出∠ BHC的度数吗?例 2:如图,已知△ABC三个内角的平分线相交于点O,OG⊥ AB,垂足为 G,∠ 1=∠ AOE,∠ 2=∠ BOG,试说明∠ 1=∠ 2. 练习: 1、若等腰三角形一腰上的高与另一腰的夹角为45° ,则这个等腰三角形的底角为 2 、如图,已知∠ MON= , 点A、B分别在射线ON、OM上移动(不与O重合),AC平分∠OAB,BD平分∠ABM,直线AC、BD交于点C。试问:随着A、B点的移动变化,∠ACB的大小是否也随之变化?若变化,说明理由;若不变求出其值。3、如图所示, CE平分∠ ACD,F为 CA延长线上一点,FG∥CE交 AB 于点 G,∠ ACD= 100° , ∠AGF=20° , 求出∠ B的度数?灿若寒星制作灿若寒星制作二、有关面积的问题例 1:如图所示,已知在△ABC中, AB=AC=8, P 是 BC上任意一点, PD⊥AB于点D,PE⊥AC于点 E. 若△ ABC的面积为 14,问: PD+PE的值是否确定?若能确定,是多少?若不能确定,请说明理由. 例 2:如图,△ ABC面积为 1,第一次操作:分别延长AB,BC,CA至点 A1,B1,C1,使 A1B=AB,B1C= BC,C1A=CA,顺次连结A1,B1,C1,得到△ A1B1C1. 第二次操作:分别延长A1B1,B1C1,C1A1至点 A2,B2,C2,使 A2B1= A1B1,B2C1= B1C1,C2A1= C1A1,顺次连结 A2,B2,C2,得到△ A2B2C2,⋯,按此规律,要使得到的三角形的面积超过2006,最少..经过次操作 . 练习:1、如图,某校有一块三角形空地,要在上面栽 种 四 种 不 同 的 花草,需...