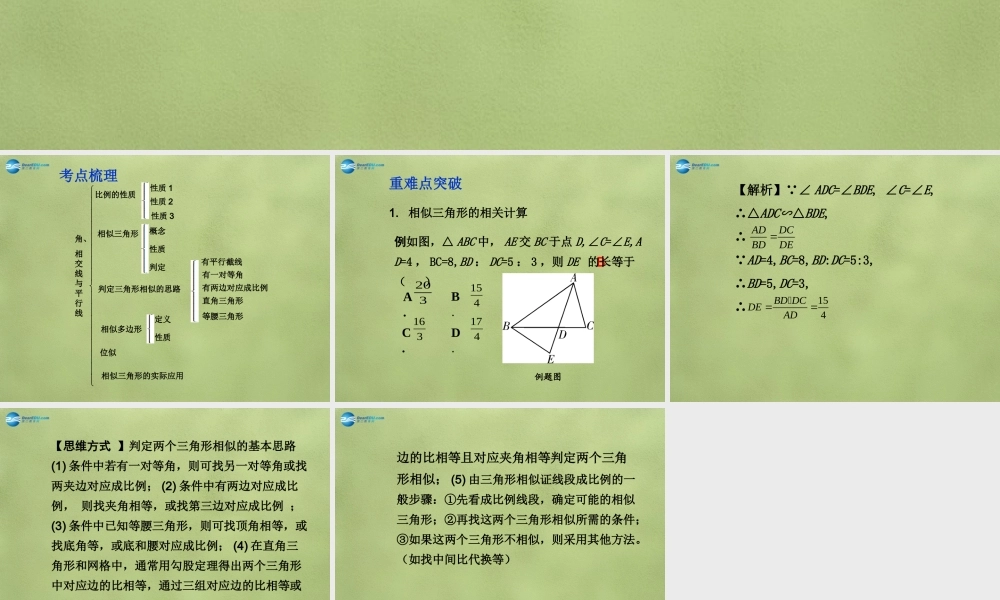
第一部分 考点研究第四章 三角形第四节 相似三角形角、相交线与平行线比例的性质 相似三角形 判定三角形相似的思路 相似多边形 位似 相似三角形的实际应用 概念 性质 判定 有平行截线 有一对等角有两边对应成比例直角三角形等腰三角形定义 性质 性质 1 性质 2 性质 3 考点梳理1. 相似三角形的相关计算 重难点突破B例如图,△ ABC 中, AE 交 BC 于点 D,∠C=∠E,AD=4 , BC=8,BD : DC=5 : 3 ,则 DE 的长等于( )例题图415320417A.B.C.D.316【解析】∵∠ ADC=∠BDE, ∠C=∠E, ∴△ADC∽△BDE,∴∵AD=4,BC=8,BD:DC=5:3,∴BD=5,DC=3,∴ADDCBDDE154BD DCDEAD【思维方式 】判定两个三角形相似的基本思路 (1) 条件中若有一对等角,则可找另一对等角或找两夹边对应成比例; (2) 条件中有两边对应成比例, 则找夹角相等,或找第三边对应成比例 ;(3) 条件中已知等腰三角形,则可找顶角相等,或找底角等,或底和腰对应成比例; (4) 在直角三角形和网格中,通常用勾股定理得出两个三角形中对应边的比相等,通过三组对应边的比相等或两组对应边的比相等且对应夹角相等判定两个三角形相似; (5) 由三角形相似证线段成比例的一般步骤:①先看成比例线段,确定可能的相似三角形;②再找这两个三角形相似所需的条件;③如果这两个三角形不相似,则采用其他方法。(如找中间比代换等)