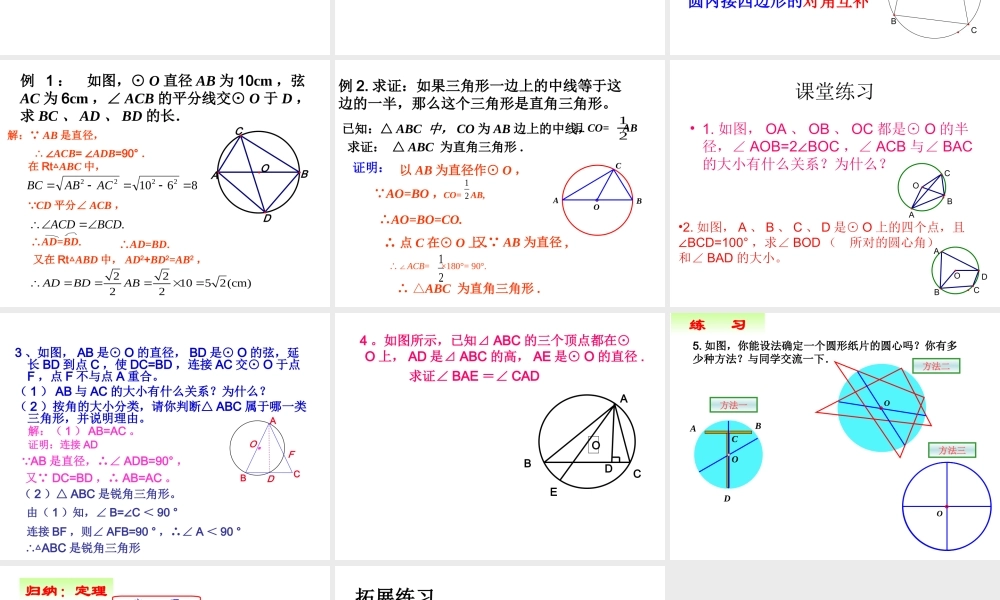
24.1.4 圆周角 复习 在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.圆 周 角定理 在同圆或等圆中,相等的圆周角所对的弧相等推 论ABCODE 问题 1 :如图, AB 是⊙ O 的直径,请问:∠C1、∠ C2、∠ C3的度数是 。ABOC1C2C3 推论:半圆(或直径)所对的圆周角是直角;90° 的圆周角所对的弦是直径。 问题 2 : 若∠ C1、∠ C2、∠ C3是直角,那么∠ AOB 是 。90°180°探究与思考:你能得出什么结论? 1 。如图 AB 是⊙ O 的直径 , C ,D 是圆上的两点 , 若∠ ABD=40°, 则∠ BCD= _____ .ABOCD40°50°练一练50° 2 。如图,∠ D=50° , ∠ ABC=60 °BD 是⊙ O 的直径,则∠ AEB 等于( )A 、 70° ; B 、 110° ;C 、 90° ; D 、 120°BACBODE 3 。判断正误:1. 同弧或等弧所对的圆周角相等( )2. 相等的圆周角所对的弧相等( )3.90° 角所对的弦是直径( )4. 直径所对的角等于 90° ( )5. 长等于半径的弦所对的圆周角等于 30° ( )√ 圆内接多边形: 如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆如图,四边形 ABCD 是⊙ O 的内接四边形, ⊙ O是四边形 ABCD 的外接圆,则∠ A 与 ∠ C 数量上有什么关系? ∠ B 与 ∠ D 呢?ABCD由此你能得出什么结论?圆内接四边形的对角互补 例 1 : 如图,⊙ O 直径 AB 为 10cm ,弦AC 为 6cm ,∠ ACB 的平分线交⊙ O 于 D ,求 BC 、 AD 、 BD 的长.86102222ACABBC又在 Rt△ABD 中, AD2+BD2=AB2 ,22105 2(cm)22ADBDAB解: AB 是直径, ∴ ∠ACB= ∠ADB=90° .在 Rt△ABC 中, CD 平分∠ ACB ,∴AD=BD..ACDBCDOABCD∴AD=BD. 例 2. 求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。·ABCO求证: △ ABC 为直角三角形 .证明:CO= AB,12以 AB 为直径作⊙ O , AO=BO ,∴AO=BO=CO.∴ 点 C 在⊙ O 上 .又 AB 为直径 ,∴∠ACB= ×180°= 90°.12已知:△ ABC 中, CO 为 AB 边上的中线,12且 CO= AB∴ △ABC 为直角三角形 . 课堂练习• 1. 如图, OA 、 OB 、 OC 都是⊙ O 的半径,∠ AOB=2 BOC∠,∠ ACB 与...