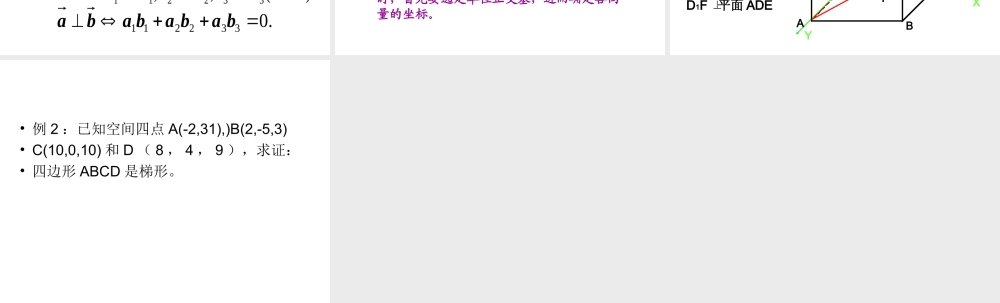
3.1.4 空间向量的坐标表示空间直角坐标系空间直角坐标系 ..向量的直角坐标运算向量的直角坐标运算 .. 一、空间直角坐标系 单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为 1 ,则这个基底叫做单位正交基底,常用来 i , j , k 表示 空间直角坐标系:在空间选定一点 O和一个单位正交基底 i 、 j 、 k 。以点 O为原点,分别以 i 、 j 、 k 的正方向建立三条数轴: x 轴、 y 轴、 z 轴,它们都叫做坐标轴 . 这样就建立了一个空间直角坐标系 O--xyz 点 O 叫做原点,向量 i 、 j 、 k 都叫做坐标向量 . 通过每两个坐标轴的平面叫做坐标平面。 二、向量的直角坐标aaaa=( 1 , 2, 3) 给定一个空间坐标系和向量 , 且设 i 、 j 、 k 为坐标向量,由空间向量基本定理,存在唯一的有序实数组 ( 1, 2, 3) 使 = 1i+ 2j+ 3k 有序数组 ( 1, 2, 3) 叫做 在空间直角坐标系 O--xyz 中的坐标,记作 .aaaaaaaaaaaaxyzOA(x,y,z)ijka 在空间直角坐标系 O--xyz 中,对空间任一点, A, 对应一个向量 OA ,于是存在唯一的有序实数组 x,y,z ,使 OA=xi+yj+zk 在单位正交基底 i, j, k 中与向量 OA 对应的有序实数组 (x,y,z) ,叫做点 A 在此空间直角坐标系中的坐标,记作 A(x,y,z) ,其中 x 叫做点A 的横坐标, y 叫做点 A 的纵坐标, z 叫做点 A的竖坐标 . 三、向量的直角坐标运算 .),,(),,,(321321bbbbaaaa设则);,,(332211babababa);,,(332211babababa);)(,,(321Raaaa;332211babababa)(,,//332211Rbabababa.0332211babababa 设 A(x1,y1,z1),B(x2,y2,z2), 则AB=OB-OA=(x2,,y2,z2)-(x1,y1,z1) =(x2-x1,y2-y1,z2-z1). 一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标 . 空间向量坐标运算法则,关键是注意空间几何关系与向量坐标关系的转化,为此在利用向量的坐标运算判断空间几何关系时,首先要选定单位正交基,进而确定各向量的坐标。 XYZABCD1A1B1C1DEF例 2 在正方体ABCD—A1B1C1D1 中 E 、 F分别是 BB1 、CD 的中点 ,求证:D1F 平面 ADE例 1 已知 a=(2,-3,5),b=(-3,1,-4), 求 a+b,a-b,8a,a b • 例 2 :已知空间四点 A(-2,31),)B(2,-5,3)• C(10,0,10) 和 D ( 8 , 4 , 9 ),求证:• 四边形 ABCD 是梯形。