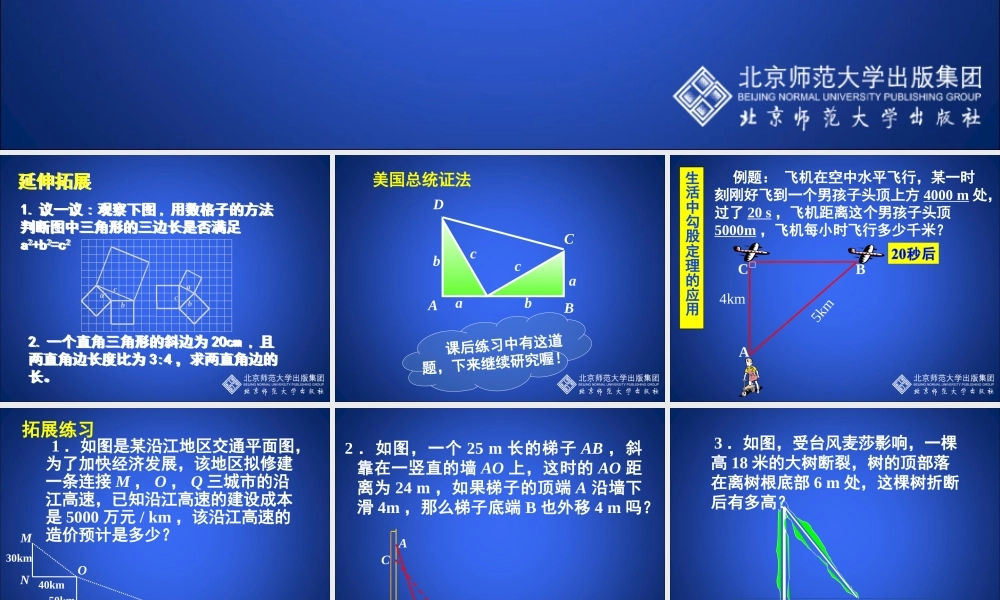
第一章 勾股定理1. 探索勾股定理(第 2 课时)2. 一个直角三角形的斜边为 20cm , 且两直角边长度比为 3:4 ,求两直角边的长。 2. 一个直角三角形的斜边为 20cm , 且两直角边长度比为 3:4 ,求两直角边的长。 1. 议一议 : 观察下图 , 用数格子的方法判断图中三角形的三边长是否满足a2+b2=c21. 议一议 : 观察下图 , 用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2ccbbaa延伸拓展延伸拓展 美国总统证法bcabcaABCD 课后练习中有这道题,下来继续研究喔!生活中勾股定理的应用 例题: 飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方 4000 m 处,过了 20 s ,飞机距离这个男孩子头顶5000m ,飞机每小时飞行多少千米?4km5kmABC拓展练习 1 .如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接 M , O , Q 三城市的沿江高速,已知沿江高速的建设成本是 5000 万元 / km ,该沿江高速的造价预计是多少?MPNOQ30km40km50km120km2 .如图,一个 25 m 长的梯子 AB ,斜靠在一竖直的墙 AO 上,这时的 AO 距离为 24 m ,如果梯子的顶端 A 沿墙下滑 4m ,那么梯子底端 B 也外移 4 m 吗?ABOCD 3 .如图,受台风麦莎影响,一棵高 18 米的大树断裂,树的顶部落在离树根底部 6 m 处,这棵树折断后有多高? 6 m通过本节课的学习你有何收获呢? 课堂小结( 2 )上网或查阅有关书籍,搜集至少 1种勾股定理的其它证法,至少 1 个勾股定理的应用问题,一周后进行展评. 布置作业( 1 )习题 1.2 1 , 2 , 3 题.