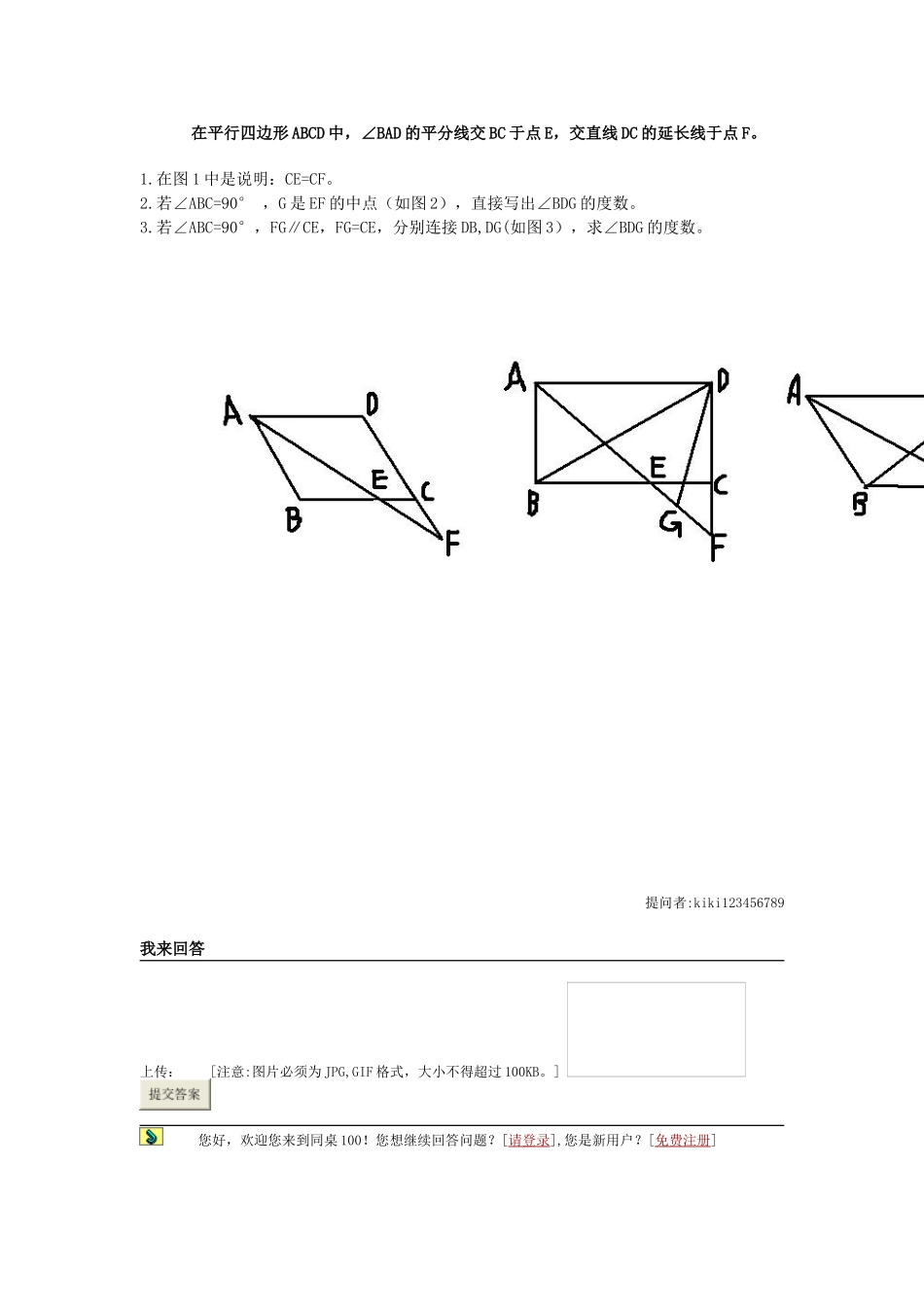
在平行四边形 ABCD 中,∠BAD 的平分线交 BC 于点 E,交直线 DC 的延长线于点 F。1.在图 1 中是说明:CE=CF。2.若∠ABC=90° ,G 是 EF 的中点(如图 2),直接写出∠BDG 的度数。3.若∠ABC=90°,FG∥CE,FG=CE,分别连接 DB,DG(如图 3),求∠BDG 的度数。提问者:kiki123456789我来回答上传: [注意:图片必须为 JPG,GIF 格式,大小不得超过 100KB。] 您好,欢迎您来到同桌 100!您想继续回答问题?[请登录],您是新用户?[免费注册] 回答因为是平行四边形,所以∠F=∠BAE,∠DAF=∠AEB又因为 AF 是角平分线所以∠BAE=∠DAF所以∠F=∠AEB又因为∠CEF=∠AEB所以∠F=∠CEF所以 CE=CF(2)因为 AF 是角平分线∠ABC=90°平行四边形所以 BE=AB又因 AB=CD所以 BE=CD连接 CG,BG因为 EFG 是等腰直角三角形所以 CG=GE又因∠GCD=∠GEB=135°CD=BE所以△BEG≌△DCG所以 BG=CD又因∠CGD+∠EGD=90°∠CGD=∠EGB所以∠EGB+∠EGD=90°所以∠BGD=90°又因 BG=GD所以△BGD 是等腰直角三角形所以∠BDG=45°3)延长 AB、FG 交于 H,连接 HD.易证四边形 AHFD 为平行四边形∵∠ABC=120°,AF 平分∠BAD∴∠DAF=30°,∠ADC=120°,∠DFA=30°∴△DAF 为等腰三角形∴AD=DF∴平行四边形 AHFD 为菱形∴△ADH,△DHF 为全等的等边三角形∴DH=DF∠BHD=∠GFD=60°∵FG=CE,CE=CF,CF=BH ∴BH=GF ∴△BHD 与△GFD 全等∴∠BDH=∠GDF∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°