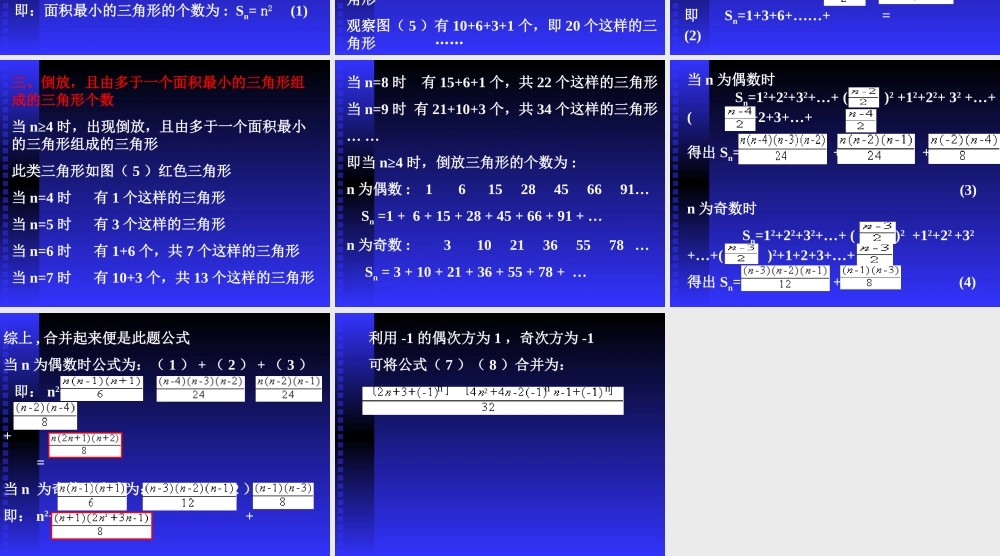
数“三角形” 徐州市撷秀中学初三( 2 )班 胡翔宇 王宇翀 指导老师:李少荣 12345 原题:(根据徐州市 2002—2003 学年度第一学期期末考试题改编)观察各图图( 1 )中面积最小的三角形有 个,共有 个三角形;图( 2 )中面积最小的三角形有 个,共有 个三角形 ;图( 3 )中面积最小的三角形有 个,共有 个三角形 ;图( 4 )中面积最小的三角形有 个,共有 个三角形 ;图( 5 )中面积最小的三角形有 个,共有 个三角形 ;此题答案分别为: 1 、 1 ; 4 、 5 ; 9 、 13 ; 16 、 27 ; 25 、 48 。但如果行数为 n 、那么共有几个三角形呢?(用化简后的 n 表示) 我们不妨将 此题分成三种情况,分别推出公式,然后再将三部分公式合并起来,得出此题公式。一、面积最小的三角形的个数二、正放,且由多于一个面积最小的三 角形组成三角形的个数三、倒放,且由多于一个面积最小的 三角形组成的三角形个数 一、面积最小的三角形的个数 观察图( 1 )~( 5 )不难发现,面积最小的三角形的个数为: 1=12 1+3=22 1+3+5=32 1+3+5+7+9=42 …… 1+3+5+7+9+……+(2n-1)=n2 即:面积最小的三角形的个数为 : Sn= n2 (1) 二、正放,且由多于一个面积最小的三角形组成三角形的个数此类三角形例如图( 4 )中的红色三角形观察图( 1 )没有这样的三角形观察图( 2 )有 1 个这样的三角形观察图( 3 )有 3+1 个,即 4 个这样的三角形观察图( 4 )有 6+3+1 个 ,即 10 个这样的三角形观察图( 5 )有 10+6+3+1 个,即 20 个这样的三角形 …… 得到一个数列:1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , 45 ,55……此数列第一个数为: 1 , 第二个数为: 1+2 第三个数为: 1+2+3 , ……,第 n 个数为: 1+2+3+4+……+n即:当行数为 n 时, Sn 值为此数列前( n-1 )个数之和。即 Sn=1+3+6+……+ = (2) 三、倒放,且由多于一个面积最小的三角形组成的三角形个数当 n≥4 时,出现倒放,且由多于一个面积最小的三角形组成的三角形此类三角形如图( 5 )红色三角形当 n=4 时 有 1 个这样的三角形当 n=5 时 有 3 个这样的三角形当 n=6 时 有 1+6 个,共 7 个这样的三角形当 n=7 时 有 10+3 个,共 13 个这样的三角形 当 n=8 时 有 15+6+1 个,共 22 个这样的三角形当...