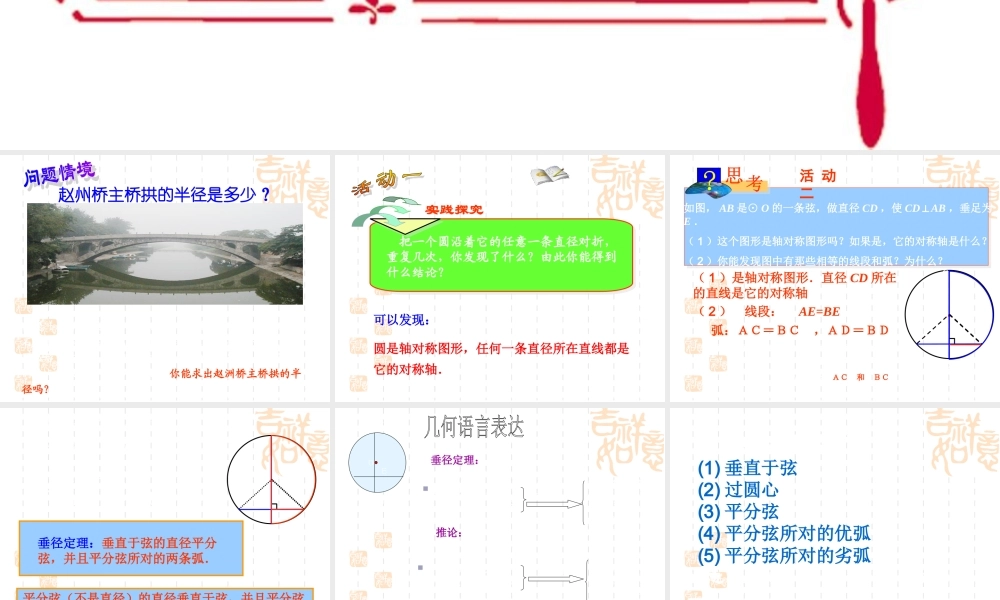
问题 :你知道赵州桥吗 ? 它是 1300 多年前我国隋代建造的石拱桥 , 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形 , 它的跨度 ( 弧所对的弦的长 ) 为 37.4m, 拱高 ( 弧的中点到弦的距离 ) 为 7.2m ,你能求出赵洲桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 实践探究 把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?可以发现:圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 如图, AB 是⊙ O 的一条弦,做直径 CD ,使 CD⊥AB ,垂足为E .( 1 )这个图形是轴对称图形吗?如果是,它的对称轴是什么?( 2 )你能发现图中有那些相等的线段和弧?为什么?·OABCDE活 动 二( 1 )是轴对称图形.直径 CD 所在的直线是它的对称轴( 2 ) 线段: AE=BE⌒⌒弧:AC=BC ,AD=BD⌒⌒把圆沿着直径 CD 折叠时, CD 两侧的两个半圆重合, 点 A 与点 B 重合, AE 与 BE 重合,AC 和 BC 重合,AD和 BD重合.⌒⌒⌒⌒ 直径CD平分弦AB,并且平分AB 及 ACB⌒⌒·OABCDE垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.即AE=BE AD=BD,AC=BC⌒⌒⌒⌒ ③AM=BM,由 ① CD 是直径 ② CDAB⊥可推得⌒ ⌒⑤AD=BD.⌒ ⌒④AC=BC,②CDAB,⊥由 ① CD 是直径 ③ AM=BM⌒ ⌒④AC=BC,⌒ ⌒⑤AD=BD.可推得DCABEO垂径定理:推论: “ 知二推三” (1) 垂直于弦 (2) 过圆心 (3) 平分弦 (4) 平分弦所对的优弧 (5) 平分弦所对的劣弧注意 : 当具备了 (1)(3) 时 , 应对另一 条弦增加”不是直径”的限制 . 你可以写出相应的命题吗 ? 相信自己是最棒的 !垂径定理的推论 如图 , 在下列五个条件中 :只要具备其中两个条件 , 就可推出其余三个结论 .●OABCDM└ ① CD 是直径 , ③ AM=BM, ② CDAB,⊥⌒ ⌒④AC=BC,⌒ ⌒⑤AD=BD. 垂径定理及推论●OABCDM└条件结论命题①②③④⑤①③②④⑤①④②③⑤①⑤②③④②③①④⑤②④①③⑤②⑤①③④③④①②⑤③⑤①②④④⑤①②③垂直于弦的直径平分弦 , 并且平分弦所的两条弧 .平分弦 ( 不是直径 ) 的直径垂直于弦 , 并且平 分弦所对的两条弧 .平分弦所对的一条弧的直径 , 垂直平分弦 , 并且平分弦所...