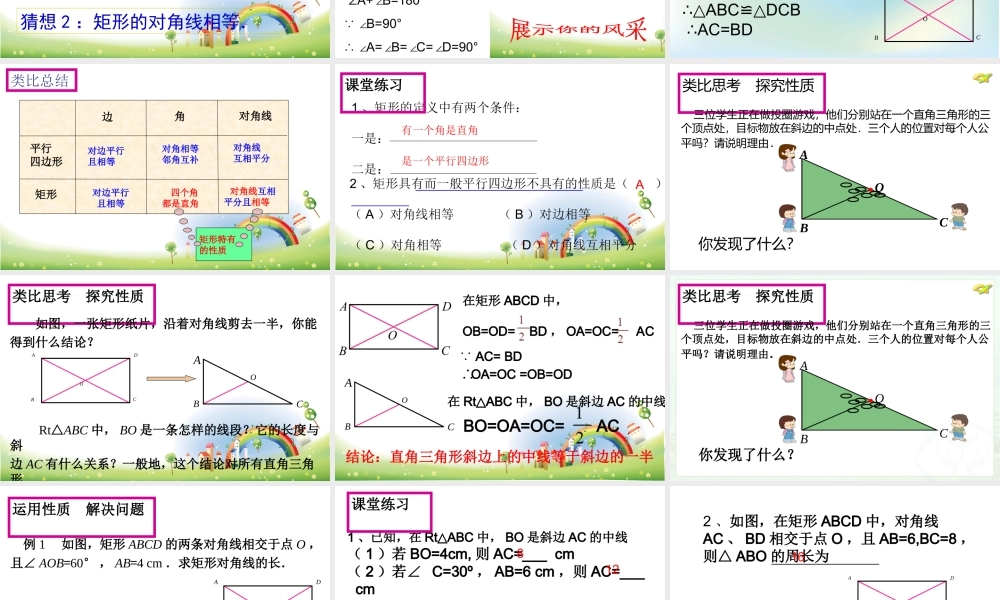
------ 矩形(矩形( 11 )) 台山市北陡中学 李振龙 1 .理解矩形的概念,明确矩形与平行四边形的区别与联系; 2 .探索并证明矩形的性质,会用矩形的性质解决简单的问题; 3 .探索并掌握“直角三角形斜边上的中线等于斜边的一半”这个定理.教学目标:观察思考 形成概念 当独木桥前后运动时,四边形 ABCD 是什么形状?当独木桥最后停下时,四边形 ABCD 有什么特殊的变化?当独木桥静止时,四边形 ABCD 是什么图形?ABDC独木桥 类比思考 探究性质 定义:有一个角是直角的平行四边形叫做矩形 ( 通常也叫做长方形)BACDABCD有一个是直角生活中有很多具有矩形形象的物品,你能举出一些例子吗?说一说,你最牛 为什么矩形的被子和床单可以反复折叠仍然是矩形?请你用一张矩形纸片做模拟实验,并说明原因 .矩形是轴对称图形,有两条对称轴矩形具有一般平行四边形的性质A B C D O 思考 : 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想 1 :矩形的四个角都是直角.猜想 2 :矩形的对角线相等. 矩形的四个角都是直角 ABDC性质1:已知:矩形 ABCD 中,∠ B=90°求证: ∠ A=∠B=∠C=∠D=90°证明: ABCD 是平行四边形 ∴ ∠A= ∠C ∠B= ∠ D ∠A+∠B=180° ∠B=90° ∴ ∠A=∠B=∠C=∠D=90°A B C D O 性质 2 :矩形的对角线相等.已知: ABCD 是矩形求证: AC=BD 证明: 四边形 ABCD 是矩形 ∴∠ ABC=DCB=90°AB=CD∠ BC=CB ABCDCB∴△≌△ ∴AC=BD 类比总结边角对角线平行四边形矩形对边平行且相等对角相等邻角互补对角线互相平分矩形特有的性质对边平行 且相等四个角都是直角对角线互相平分且相等1 、矩形的定义中有两个条件:一是: 二是: 有一个角是直角是一个平行四边形2 、矩形具有而一般平行四边形不具有的性质是( )( A )对角线相等 ( B )对边相等( C )对角相等 ( D )对角线互相平分A课堂练习 类比思考 探究性质 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处.三个人的位置对每个人公平吗?请说明理由.A B C O 你发现了什么?类比思考 探究性质 如图,一张矩形纸片,沿着对角线剪去一半,你能得到什么结论?A B C D O B C O A Rt△ABC 中, BO 是一条怎样的线段?它的长度与斜边 AC 有什么关系?一般地,这个结论...