函数最值问题解法浅谈VIP免费

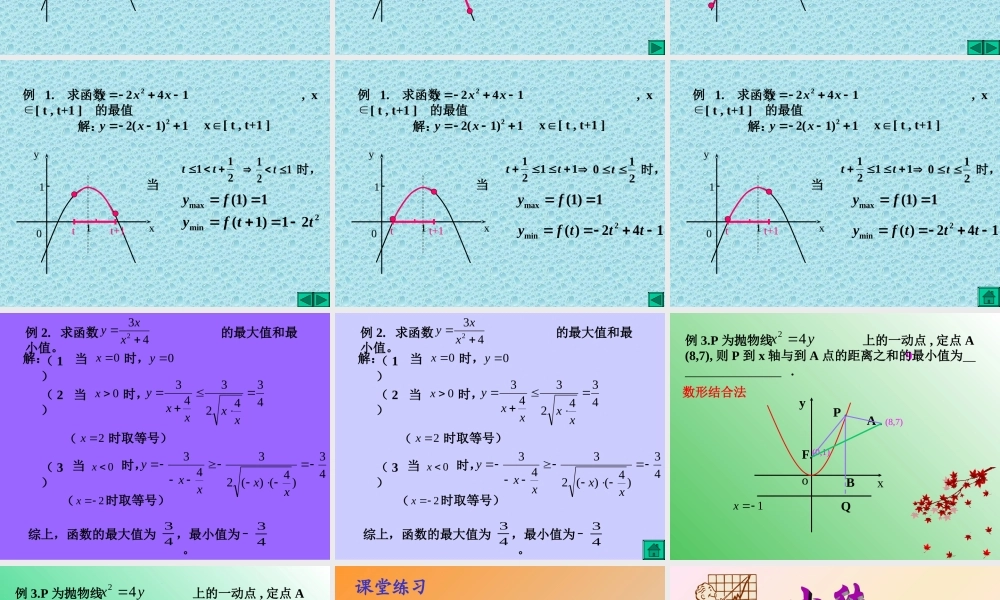
—— 求最值的常见方法( 一 )高中数学组 欧锦州 1. 配方法2. 利用基本不等式（均值不等式）5. 利用函数的单调性4. 换元转化法 6. 利用反函数的定义域等等3. 数形结合 1. 配方法2. 利用基本不等式（均值不等式）5. 利用函数的单调性4. 换元转化法 6. 利用反函数的定义域等等3. 数形结合 0xy111422xxy例 1. 求函数 在下列区间的最值 ①x[ 2 , 3 ] x[ , 2 ] ∈②∈ ③x[ t , t+1 ] ∈21解：1)1(22 xy 1422xxy例 1. 求函数 , x[ t , t+1 ] ∈的最值解：1)1(22 xyx[ t , t+1 ]∈110xy 1)1(22 xy解：x[ t , t+1 ]∈11 tt+1当 t > 1 时 , 142)(2maxtttfy2min21)1(ttfy0xy1422xxy例 1. 求函数 , x[ t , t+1 ] ∈的最值 11tt+1当 t +1< 1 即 t < 0 时142)(2mintttfy2max21)1(ttfy0xy1422xxy例 1. 求函数 , x[ t , t+1 ] ∈的最值1)1(22 xy解：x[ t , t+1 ]∈ 11tt+1 当 211tt121t时，1)1(max fy2min21)1(ttfy0xy1)1(22 xy解：x[ t , t+1 ]∈1422xxy例 1. 求函数 , x[ t , t+1 ] ∈的最值 11tt+1 当 1121tt210t时，1)1(max fy142)(2mintttfy0xy1422xxy例 1. 求函数 , x[ t , t+1 ] ∈的最值1)1(22 xy解：x[ t , t+1 ]∈ 11tt+1 当 1121tt210t时，1)1(max fy142)(2mintttfy0xy1422xxy例 1. 求函数 , x[ t , t+1 ] ∈的最值1)1(22 xy解：x[ t , t+1 ]∈ 例 2. 求函数 的最大值和最小值。432 xxy解：当0x时，0y（ 1）当0x时，（ 2）4342343xxxxy2x时取等号）（（ 3）当时，0x43)4()(2343xxxxy时取等号）（2x综上，函数的最大值为，最小值为 。4343 例 2. 求函数 的最大值和最小值。432 xxy解：当0x时，0y（ 1）当0x时，（ 2）4342343xxxxy2x时取等号）（（ 3）当时，0x43)4()(2343xxxxy时取等号）（2x综上，函数的最大值为，最小值为 。4343 xyoF.(0,1)A . (8,7)P .9数形结合法1x例 3.P 为抛物线 上的一动点...