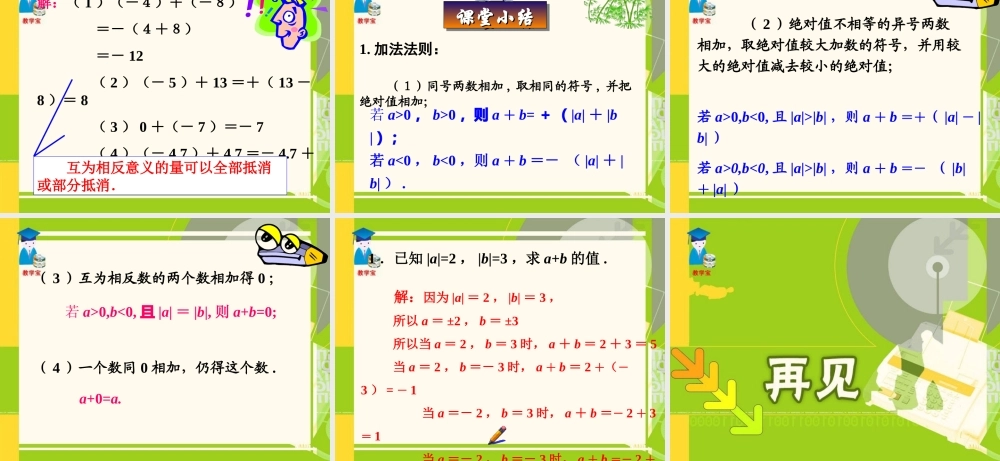
复习:以向东走为正,则向东走 30 米,可用有理数表示为:则向西走 20 米,可用有理数表示为: 小刚在一条东西向的跑道上,先走了 30 米,又走了 20 米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米? 1 .若两次都向东,一共向东走了多少米? (+ 30 )+(+ 20 )=+ 50- 10 0 10 20 30 40 50 + 30 +20+ 502 .若两次都向西,一共向西走了多少米? (- 30 )+(- 20 )=- 50 - 50 - 40 - 30 - 20 - 10 0 - 20 -30- 50 3 .若第一次向东走 20 米,第二次向西走 25 米,那他现在在什么位置?( + 20) + ( - 25) =- 5 - 40 - 30 - 20 - 10 0 10 20 - 25 +20- 5 4 .若第一次向西走 25 米,第二次向东走 10 米,那他现在在什么位置?( - 25) + ( + 10) = - 15 - 30 - 20 - 10 0 10 20 30 - 25 +10- 15 5 .若第一次向西走 20 米,第二次向东走 20 米,那他现在在什么位置?( - 20) + ( + 20) = 0 - 50 - 40 - 30 - 20 - 10 0 + 20 -20 6 .若第一次向东走 30 米,第二次站在原地没动,那他现在在什么位置?( + 30) + 0 =+ 30- 10 0 10 20 30 40 50 + 30+ 30有理数加法有没有规律? 1 .和的符号与两个加数的符号有什么关系? 2 .和的绝对值与两个加数的绝对值又有什么关系? 观察、比较下面几个式子,看能否从这些算式中得到启发,想办法归纳出有理数加法的法则? (+ 30 )+(+ 20 )=+ 50(- 30 )+(- 20 )=- 50( 20 )+( 25 )= 5( 25 )+ (10 )= 15( 20 )+( 20 )= 0(+ 30 )+ 0 =+ 30有理数加法法则: 1 .同号两数相加,取相同的符号,并把绝对值相加. 2 .绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得 0 . 3 .一个数同 0 相加,仍得这个数.知识要点知识要点知识要点知识要点例 1 :计算:( 1 )(-4)+(-8);( 2 )(- 5 )+ 13 ;( 3 ) 0 +(- 7 ); ( 4 )(- 4.7 )+ 3.9 .解:( 1 )(-4)+(-8) =-(4+8) =- 12 ( 2 )(- 5 )+...