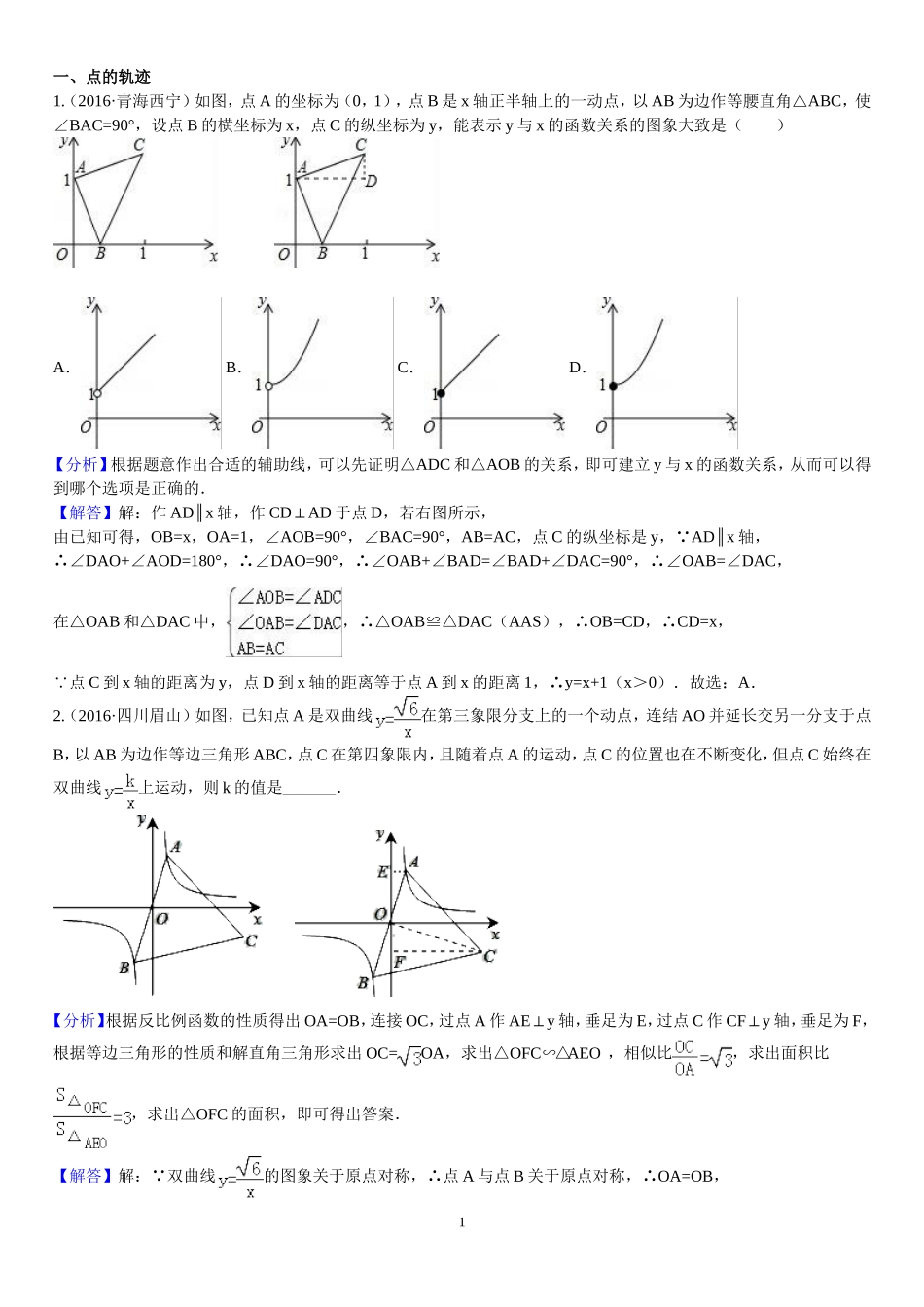
一、点的轨迹1.(2016·青海西宁)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是()A.B.C.D.【分析】根据题意作出合适的辅助线,可以先证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而可以得到哪个选项是正确的.【解答】解:作ADx∥轴,作CDAD⊥于点D,若右图所示,由已知可得,OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y, ADx∥轴,DAO+AOD=180°∴∠∠,∴∠DAO=90°,∴∠OAB+BAD=BAD+DAC=90°∠∠∠,∴∠OAB=DAC∠,在△OAB和△DAC中,,∴△OABDAC≌△(AAS),∴OB=CD,∴CD=x, 点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1,∴y=x+1(x>0).故选:A.2.(2016·四川眉山)如图,已知点A是双曲线在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线上运动,则k的值是.【分析】根据反比例函数的性质得出OA=OB,连接OC,过点A作AEy⊥轴,垂足为E,过点C作CFy⊥轴,垂足为F,根据等边三角形的性质和解直角三角形求出OC=OA,求出△OFCAEO∽△,相似比,求出面积比,求出△OFC的面积,即可得出答案.【解答】解: 双曲线的图象关于原点对称,∴点A与点B关于原点对称,∴OA=OB,1连接OC,如图所示, △ABC是等边三角形,OA=OB,∴OCAB⊥.∠BAC=60°,∴tanOAC=∠=,∴OC=OA,过点A作AEy⊥轴,垂足为E,过点C作CFy⊥轴,垂足为F, AEOE⊥,CFOF⊥,OCOA⊥,AEO=OFC∴∠∠,∠AOE=90°FOC=OCF﹣∠∠,∴△OFCAEO∽△,相似比,∴面积比, 点A在第一象限,设点A坐标为(a,b), 点A在双曲线上,∴SAEO△=ab=,∴SOFC△=FC•OF=,∴设点C坐标为(x,y), 点C在双曲线上,∴k=xy, 点C在第四象限,∴FC=x,OF=y﹣.FC•OF=x•∴(﹣y)=xy=﹣﹣,故答案为:﹣3.3.如图,正方形ABCD的边长为8,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向D点运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长。依题意画出图形,如图所示.此时在Rt△APQ中,O为PQ的中点,所以AO=PQ=4.所以点O在以A为圆心,半径为4,圆心角为90°的圆弧上.PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如图所示:所以PQ的中点O所经过的路径的长为:×2π×4=6π;4.(2014年山东烟台)在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明)(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;(4)如图④,当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最小值.2【解答】解:(1)AE=DF,AE⊥DF.理由: 四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°. DE=CF,∴△ADE≌△DCF.∴AE=DF,∠DAE=∠CDF,由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.∴AE⊥DF;(2)是;(3)成立.理由:由(1)同理可证AE=DF,∠DAE=∠CDF延长FD交AE于点G,则∠CDF+∠ADG=90°,∴∠ADG+∠DAE=90°.∴AE⊥DF;(4)如图:由于点P在运动中保持∠APD=90°,∴点P的路径是一段以AD为直径的弧,设AD的中点为O,连接OC交弧于点P,此时CP的长度最小,在Rt△ODC中,OC=,∴CP=OC﹣OP=.5.(2016·南充)已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBCPAM∽△,延长BP交AD于点N,连结CM.(1)如图一,若点M在线段AB上,求证:APBN⊥;AM=AN;(2)①如图二,在点P运动过程中,满足△PBCPAM∽△的点M在AB的延长线上时,APBN⊥...