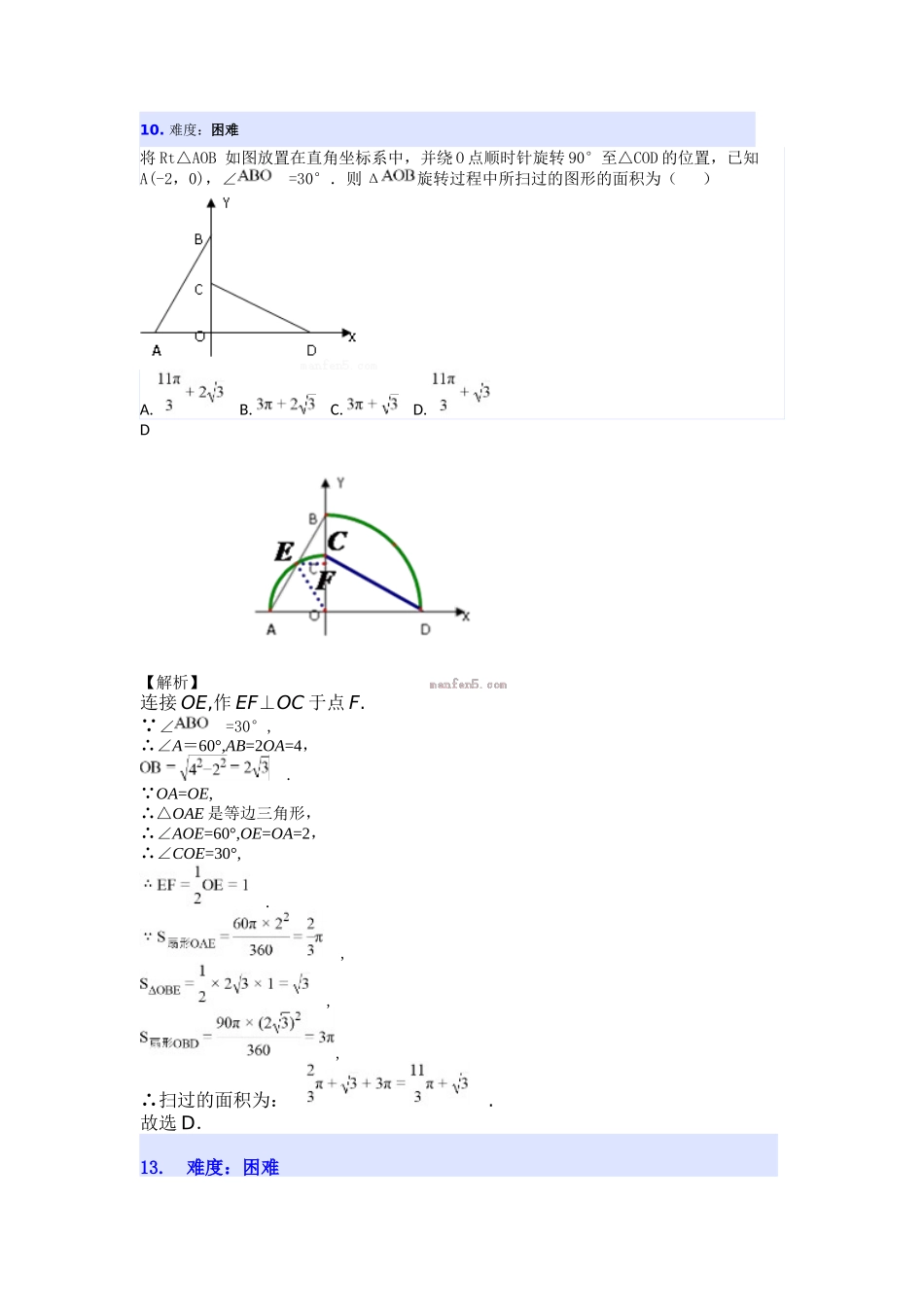
10.难度:困难将Rt△AOB如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠=30°.则Δ旋转过程中所扫过的图形的面积为()A.B.C.D.D【解析】连接OE,作EF⊥OC于点F. ∠=30°,∴∠A=60°,AB=2OA=4,. OA=OE,∴△OAE是等边三角形,∴∠AOE=60°,OE=OA=2,∴∠COE=30°,.,,,∴扫过的面积为:.故选D.13.难度:困难如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到CD的距离为()A.cmB.3cmC.3cmD.6cmA【解析】试题分析:连接BC,根据垂径定理知圆心O到弦CD的距离为OE;由圆周角定理知∠COB=2∠CDB=60°,已知半径OC=5,即可在Rt△OCE中求OE=.故选:A14.难度:中等如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为()A.1B.2C.3D.4C【解析】试题分析:作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.∴EP+FP=EP+FP′.由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+FP=EF′′. 四边形ABCD为菱形,周长为12,∴AB=BC=CD=DA=3,AB∥CD, AF=2,AE=1,∴DF=AE=1,∴四边形AEFD′是平行四边形,∴EF=AD=3′.∴EP+FP的最小值为3.故选:C.14.难度:困难如图,己知中,.动点在边上,以为边作等边(点、在的同侧).在点从点移动至点的过程中,点移动的路线长为________.【解析】如图,作EF⊥AB垂足为F,连接CF. ∠ACB=90°,∠A=30°,∴∠ABC=60°, △EBD是等边三角形,∴BE=BD,∠EBD=60°,∴∠EBD=∠ABC,∴∠EBF=∠DBC,在△EBF和△DBC中,,∴△EBF≌△DBC,∴BF=BC,EF=CD, ∠FBC=60°,∴△BFC是等边三角形,∴CF=BF=BC, BC=AB,∴BF=AB,∴AF=FB,∴点E在AB的垂直平分线上,∴在点D从点A移动至点C的过程中,点E移动的路线和点D运动的路线相等,∴在点D从点A移动至点C的过程中,点E移动的路线为.故答案为:.点睛:本题考查轨迹、等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是添加辅助线构造全等三角形,正确找到点E的运动路线,属于中考常考题型.17.难度:中等如图,在Rt△ABC中,∠C=90°,,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是______.相交【解析】连接CP.由折叠可得,MN⊥CP. ,∴CP不是直径, MN是直径,∴MN>CP. 点P在AB上,∴以MN为直径的圆与直线AB的位置关系是相交.详细信息18.难度:压轴如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一动点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使∠DCP=60°连接OD,则OD长的最大值为_____.【解析】把△OPC顺时针旋转60°,则△OCO′是等边三角形.以CO′的中点N作半径为1的圆,连接ON并延长交圆N于点F,则OF的长就是OD的最大值.,.,的最大值为.18.难度:中等如图,BC=2,A为半径为1的⊙B上一点,连接AC,在AC上方作一个正六边形ACDEFG,连接BD,则BD的最大值为___________。【解析】由正六边形的性质得出AC=CD,∠ACD=120°,把△ABC和⊙B绕点C旋转120°得△DHC和⊙H,BH的延长线于⊙H的交点M,作CN⊥BM于N,则BM的长度就是DB达到的最大值,∠BCH=120°,CH=CB=2,BN=HN,由等腰三角形的性质和三角形的内角和定理得出∠B=∠CHB=30°,由直角三角形的性质得出CN=BC=1,由勾股定理得出BN==,得出BH=2BN=2,求出BM=BH+HM=2+1即可.【解析】 六边形ACDEFG是正六边形,∴AC=CD,∠AC(6-2)×180°÷6=120°,把△ABC和⊙B绕点C旋转120°得△DHC和⊙H,BH的延长线与⊙H的交点为M,作CN⊥BM于N,如图所示:则BM的长度就是DB达到的最大值,∠BCH=120°,CH=CB=2,BN=HN,∴∠B=∠CHB=(180°-120°)÷2=30°,∴CN=BC=1,∴BN==,∴BH=2BN=2,∴BM=BH+HM=2+1,即BD的最大值为2+1,故答案为:2+1.“点睛”本题考查了正多边形和圆,正六边形的性质、旋转的性质、等腰三角形的性质,三角形内角和定理、勾股定理等知识;熟练掌握正六边形的性质和旋转的性质是解决问题的关键.20.难度:困难校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超...