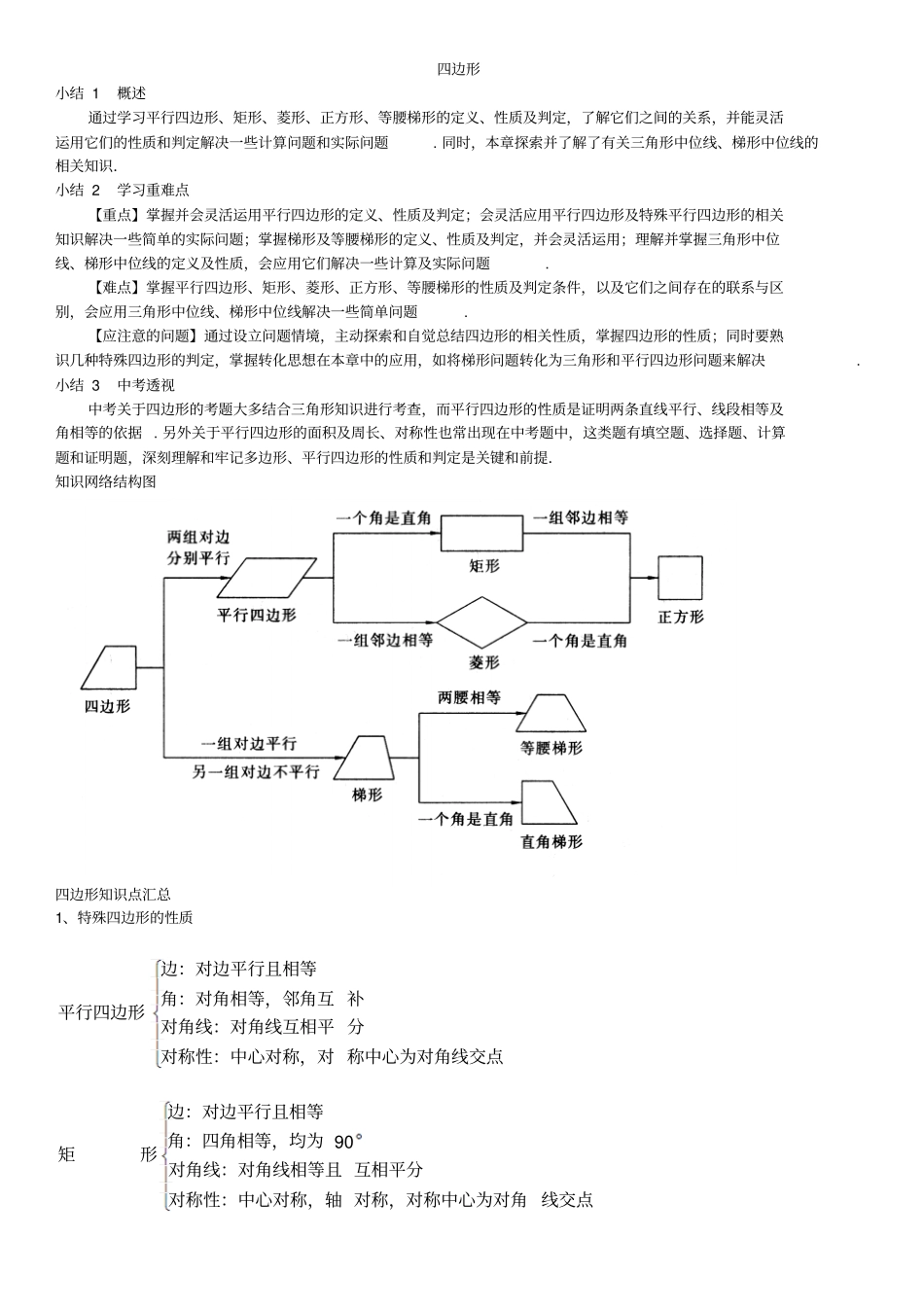
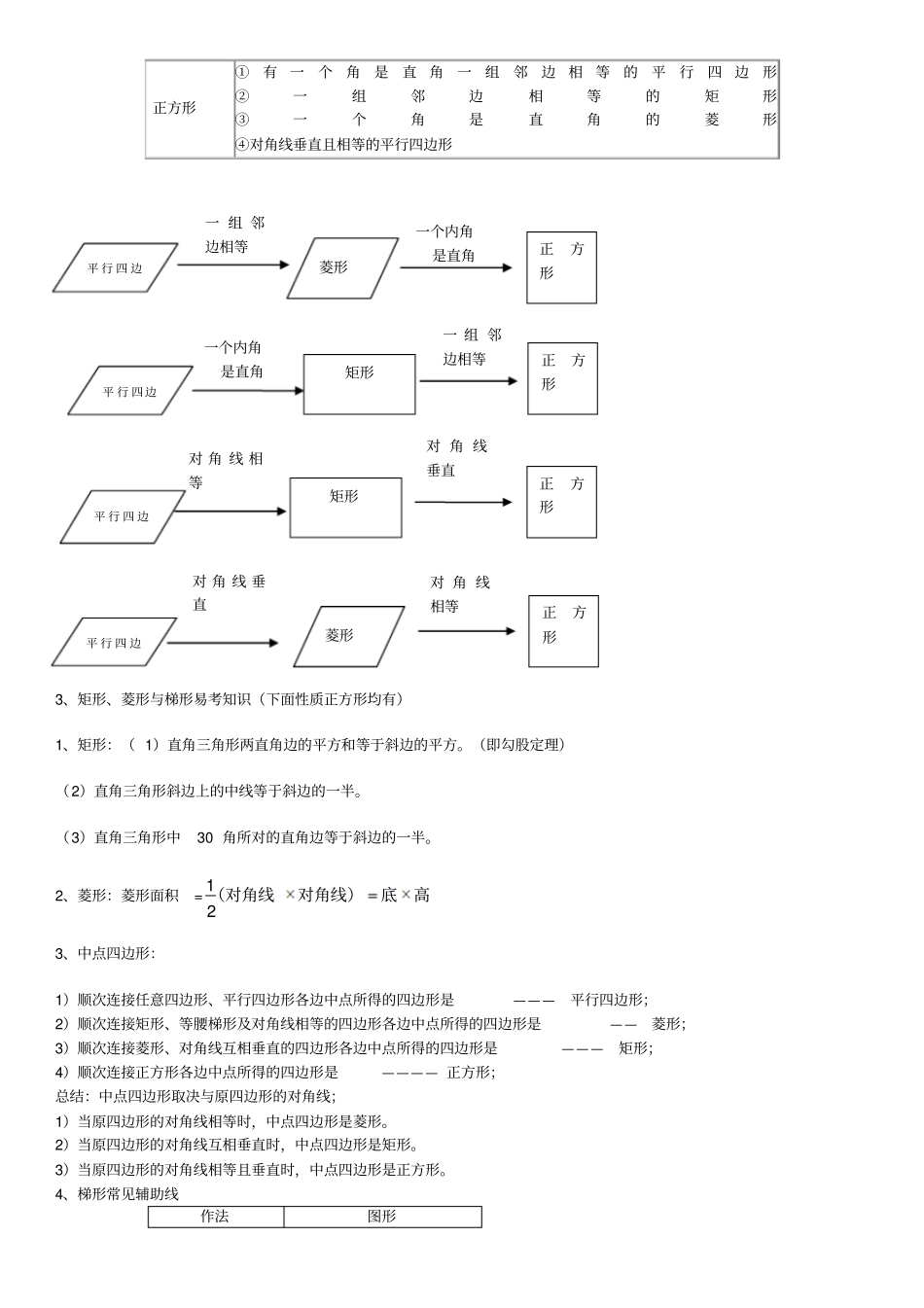
四边形小结 1 概述通过学习平行四边形、矩形、菱形、正方形、等腰梯形的定义、性质及判定,了解它们之间的关系,并能灵活运用它们的性质和判定解决一些计算问题和实际问题. 同时,本章探索并了解了有关三角形中位线、梯形中位线的相关知识.小结 2 学习重难点【重点】掌握并会灵活运用平行四边形的定义、性质及判定;会灵活应用平行四边形及特殊平行四边形的相关知识解决一些简单的实际问题;掌握梯形及等腰梯形的定义、性质及判定,并会灵活运用;理解并掌握三角形中位线、梯形中位线的定义及性质,会应用它们解决一些计算及实际问题. 【难点】掌握平行四边形、矩形、菱形、正方形、等腰梯形的性质及判定条件,以及它们之间存在的联系与区别,会应用三角形中位线、梯形中位线解决一些简单问题. 【应注意的问题】通过设立问题情境,主动探索和自觉总结四边形的相关性质,掌握四边形的性质;同时要熟识几种特殊四边形的判定,掌握转化思想在本章中的应用,如将梯形问题转化为三角形和平行四边形问题来解决. 小结 3 中考透视中考关于四边形的考题大多结合三角形知识进行考查,而平行四边形的性质是证明两条直线平行、线段相等及角相等的依据 . 另外关于平行四边形的面积及周长、对称性也常出现在中考题中,这类题有填空题、选择题、计算题和证明题,深刻理解和牢记多边形、平行四边形的性质和判定是关键和前提.知识网络结构图四边形知识点汇总1、特殊四边形的性质称中心为对角线交点对称性:中心对称,对分对角线:对角线互相平补角:对角相等,邻角互边:对边平行且相等平行四边形线交点对称,对称中心为对角对称性:中心对称,轴互相平分对角线:对角线相等且角:四角相等,均为边:对边平行且相等形矩90正方形称中心为对角线交点对称性:中心对称,对直平分,且平分对角对角线:对角线互相垂补角:对角相等,邻角互行边:四边相等,对边平形菱线交点对称,对称中心为对角对称性:轴对称,中心直平分且相等对角线:对角线互相垂为角:四角相等,每个都行边:四边相等,对边平形方正90对称图形对称性:等腰梯形为轴角平分线:相等角相等相邻角互补,同一底上角:不在同一底边上的等,另一组相等不平行边:一组对边平行不相等腰梯形相邻互补,有一组均为角:不在同一底边上的一组不平行边:一组对边平行,另直角梯形相邻角互补角:不在同一底边上的一组不平行边:一组对边平行,另一般梯形形梯90四边形图形示意图2、四种特殊四边形常用...