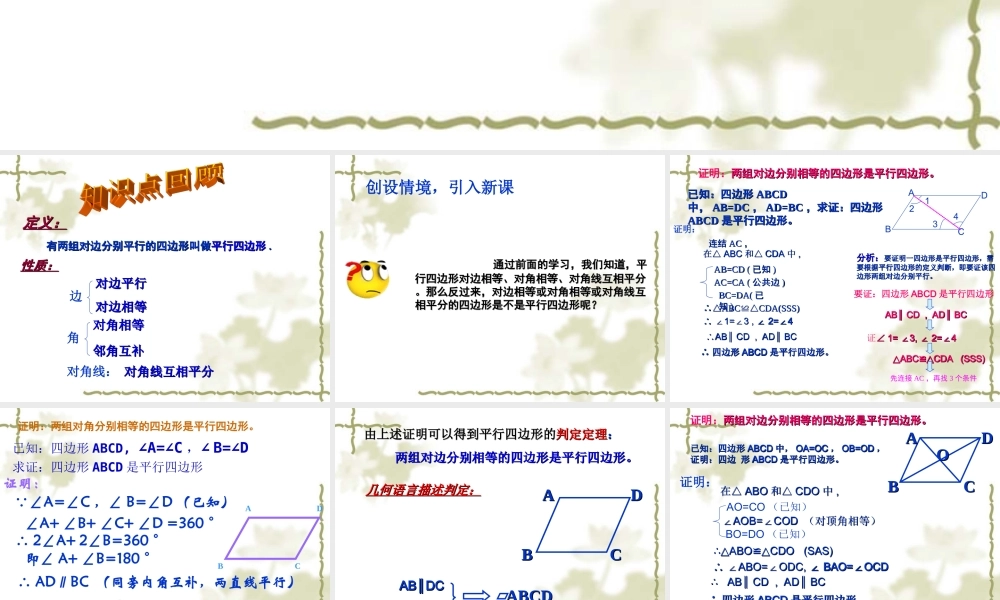
定义:定义:有两组对边分别平行的四边形叫做有两组对边分别平行的四边形叫做平行四边形平行四边形 ..性质:性质:边对边平行对边平行对边相等对边相等角对角相等对角相等邻角互补邻角互补对角线互相平分对角线互相平分对角线: 通过前面的学习,我们知道,平通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分行四边形对边相等、对角相等、对角线互相平分。那么反过来,对边相等或对角相等或对角线互。那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?相平分的四边形是不是平行四边形呢?创设情境,引入新课证明:两组对边分别相等的四边形是平行四边形。两组对边分别相等的四边形是平行四边形。已知:四边形已知:四边形 ABCDABCD中,中, AB=DCAB=DC ,, AD=BCAD=BC ,求证:四边形,求证:四边形ABCDABCD 是平行四边形。是平行四边形。分析:分析:要证明一四边形是平行四边形,需要证明一四边形是平行四边形,需要根据平行四边形的定义判断,即要证该四要根据平行四边形的定义判断,即要证该四边形两组对边分别平行。边形两组对边分别平行。要证:四边形 ABCD 是平行四边形AB CD , AD BC∥∥AB CD , AD BC∥∥证∠∠ 1= 3, 2=4∠∠∠1= 3, 2=4∠∠∠△△ABCCDA (SSS)≌△ABCCDA (SSS)≌△证明:连结连结 ACAC ,,∴△∴△ABCCDA(SSS)≌△ABCCDA(SSS)≌△在△在△ ABCABC 和△和△ CDACDA 中中 ,,AB=CD (AB=CD ( 已知已知 ))AC=CA (AC=CA ( 公共边公共边 ))BC=DA(BC=DA( 已已知知 )) ∴ ∴ ∠∠1=3 , ∠1=3 , ∠ 2=4∠∠ 2=4∠∠∴∴AB CD , AD BC∥∥AB CD , AD BC∥∥∴∴ 四边形四边形 ABCDABCD 是平行四边形。是平行四边形。ABCD1234先连接 AC ,再找 3 个条件BDAC已知:四边形 ABCD, ∠A=∠C∠,B=∠D求证:四边形 ABCD 是平行四边形 ∠A=∠C ,∠ B=∠D (已知) ∠A+ ∠B+ ∠C+ ∠D =360 °证明:∴ AD∥BC (同旁内角互补,两直线平行)同理可证 AB∥CD证明:两组对角分别相等的四边形是平行四边形。∴ 2∠A+ 2∠B=360 °即∠ A+ ∠B=180 °∴ 四边形 ABCD 是平行四边形由上述证明可以得到平行四边形的由上述证明可以得到平行四边形的判定定理判定定理::两组对边分别相等的四边形是平行四边形。两组对边分别相等的四边形是平行四边形。几何语言描述判定:几何语言描述判定:AB ...