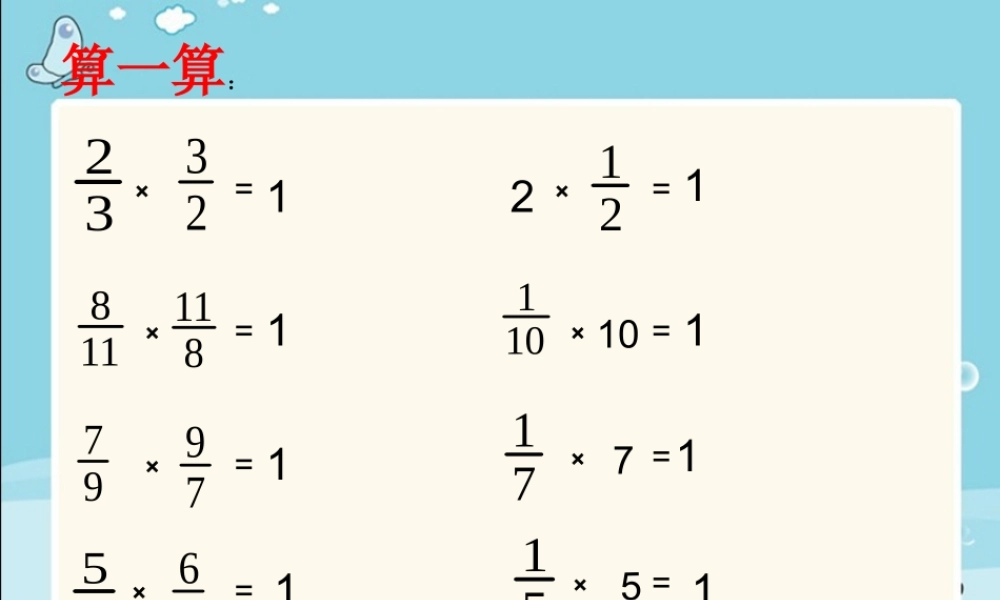3223101977971655651×2× 21118811×× 10×× 7××5算一算:========11111111 3223101977971655651×2 × 21118811××10××7×× 5========11111111( 1 )从上面的口算题中,你发现了什么?( 2 )像这样的两个数,你还能再举出一些吗? 3223101977971655651×2 × 21118811××10××7×× 5========11111111每个算式的积是 1 。 3223101977971655651×2 × 21118811××10××7×× 5========11111111 ( 3 )如果让我们给这样的一对数取个字你认为叫什么好? 倒 数 3223101977971655651×2 × 21118811××10××7×× 5========11111111 如果两个数的乘积是 1 ,那么我们称其中一个数是另一个数的倒数,并称这两个数互为倒数。 强调• 倒数是对两个数来说的,它们相互依存,必须说一个数是另一个数的倒数,不能孤立地说某一个数是倒数。 2 、哪些数有倒数? 他们谁说的对? 整数有倒数明明红红 144 可看作是14 所以 4 的倒数是 41 他们谁说的对?0 没有倒数 ,1 的倒数是本身 .明明红红 他们谁说的对?小数有倒数。小数有倒数小数没有倒数明明红红 3 、怎样求一个数的倒数? 433443342552441分子分母调换位置分子分母调换位置14分子分母调换位置= 填空。练一练 1 1)(321 23 1)(72 71 1)(913 9 1)(14 1 先说出下面每组数的倒数, 再说一说你发现了什么规律 ?练一练 243⑴5274真分数的倒数一定大于 1 。大于 1 的假分数的倒数一定小于 1 。不为 0 的整数,它的 倒数的分子一定是 1 。讨论下面的三组数:27⑵3⑷4961391521⑶101121分子是 1 的分数,它的倒数一定是整数 。 1 、 0 的倒数是 0 。2 、 是倒数。 3 、小数没有倒数。4 、 和 互为倒数。5 、 的倒数是 。251222737257( ) ( )( ) ( ) ( )判断题。练一练 3概念辨析 我能行!巩固题38⑴ 的倒数是 ( ) 。 8371⑵ 的倒数是 ( ) 。 79⑶ 的倒数是 ( ) 。 91114⑷ 的倒数是 ( ) 。 432310 ⑸ 的倒数是 ( ) 。 3.094⑹ 的倒数是 ( ) 。 25.2 理解倒数的意义,掌握求一个数的倒数的方法。 本课小结 87311399137831100151315131001把互为倒数的两个数连起来:1作业