尚建丽特殊角三角函数值的解法VIP免费

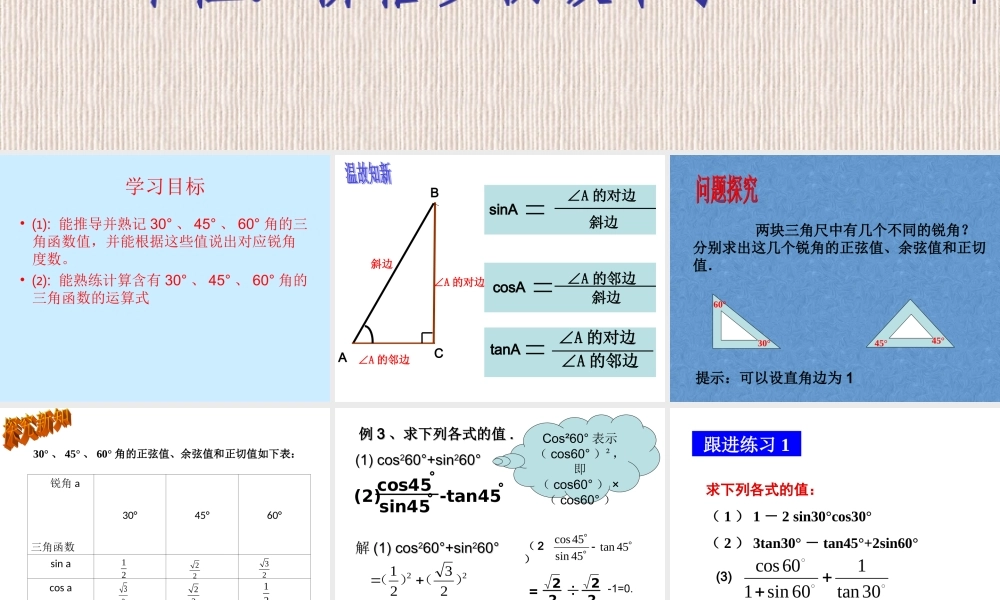
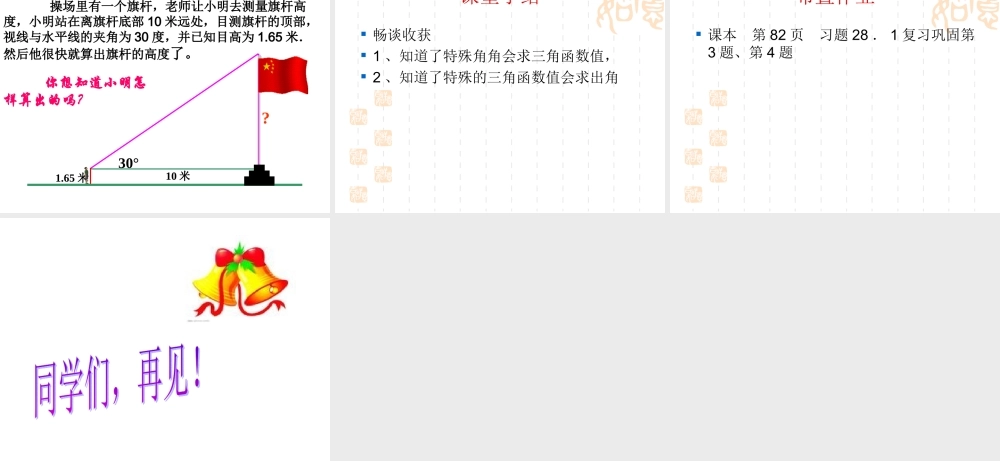
锐角三角函数（ 3 ）特殊角的三角函数值姓名：尚建丽单位：柳格乡初级中学 学习目标• ⑴: 能推导并熟记 30° 、 45° 、 60° 角的三角函数值，并能根据这些值说出对应锐角度数。• ⑵: 能熟练计算含有 30° 、 45° 、 60° 角的三角函数的运算式 AB C∠A 的对边∠A 的邻边∠A 的对边∠A 的邻边tanAcosA∠A 的邻边∠A 的对边斜边sinA斜边斜边 两块三角尺中有几个不同的锐角？分别求出这几个锐角的正弦值、余弦值和正切值．30°60°45°45°提示：可以设直角边为 1 30° 、 45° 、 60° 角的正弦值、余弦值和正切值如下表： 锐角 a三角函数30°45°60°sin acos atan a1222322212332331 例 例 33 、求下列各式的值、求下列各式的值 ..(2)cos45 sin45  -tan45 解解 (1) cos(1) cos2260°+sin60°+sin2260°60°Cos²60° 表示（ cos60° ）²，即（ cos60° ） ×（ cos60° ）（ 2） 45tan45sin45cos (1) cos(1) cos2260°+sin60°+sin2260°60°222321）（）（=12222=-1=0.跟进练习 1求下列各式的值：（ 1 ） 1 － 2 sin30°cos30°（ 2 ） 3tan30° － tan45°+2sin60°30tan160sin160cos(3) 例 例 44 、、 (1)(1) 如图，在如图，在 Rt ABC△Rt ABC△中，∠中，∠ CC=90°=90° ，， AB= ,BC= AB= ,BC= 。求∠。求∠ AA 的度数。的度数。(2)(2) 如图如图 ,, 已知圆锥的高已知圆锥的高 AOAO 等于圆锥的底面等于圆锥的底面半径半径 OBOB 的 倍的 倍 ,, 求求 α. α. 63363CAB(1)OBA(2)例 4 （ 1 ）如图，在 Rt△ABC 中，∠ C ＝ 90° ， ，求∠ A 的度数．3,6BCABABC36解：如图所示63sinA= ABBC ==22  A = 45（ 2 ）如图，已知圆锥的高 AO 等于圆锥的底面半径 OB 的 倍，求 a ．ABO3解：如图所示603OBOB3BOAOtan 当 A 、 B 为锐角时，若 A≠B ，则 sinA≠sinB ， cosA≠cosB ， tanA≠tanB. 30A33217ACBCtanA解在 Rt△ABC 中，∠ C ＝ 90° ， 求∠ A 、∠ B 的度数．21,7ACBCBAC721跟进练习 2 1 、在 Rt△ABC 中，∠ C ＝ 90° ， a=2 ，sinA= ，求 cosA 和 tanA 的值31CAB CAB2 、在 Rt△ABC 中，∠ C ＝ 90°,cosA= ,AC= , 求 BC 的长2334 操场里有一个旗杆，老师让小明去测量旗杆高度，小明站在离旗杆底部 10 米远处，目测旗杆的顶部，视线与水平线的夹角为 30 度，并已知目高为 1.65 米．然后他很快就算出旗杆的高度了。1.65 米10 米? 你想知道小明怎样算出的吗？应用生活30° 课堂小结 畅谈收获 1 、知道了特殊角角会求三角函数值， 2 、知道了特殊的三角函数值会求出角 布置作业 课本 第 82 页 习题 28 ． 1 复习巩固第3 题、第 4 题