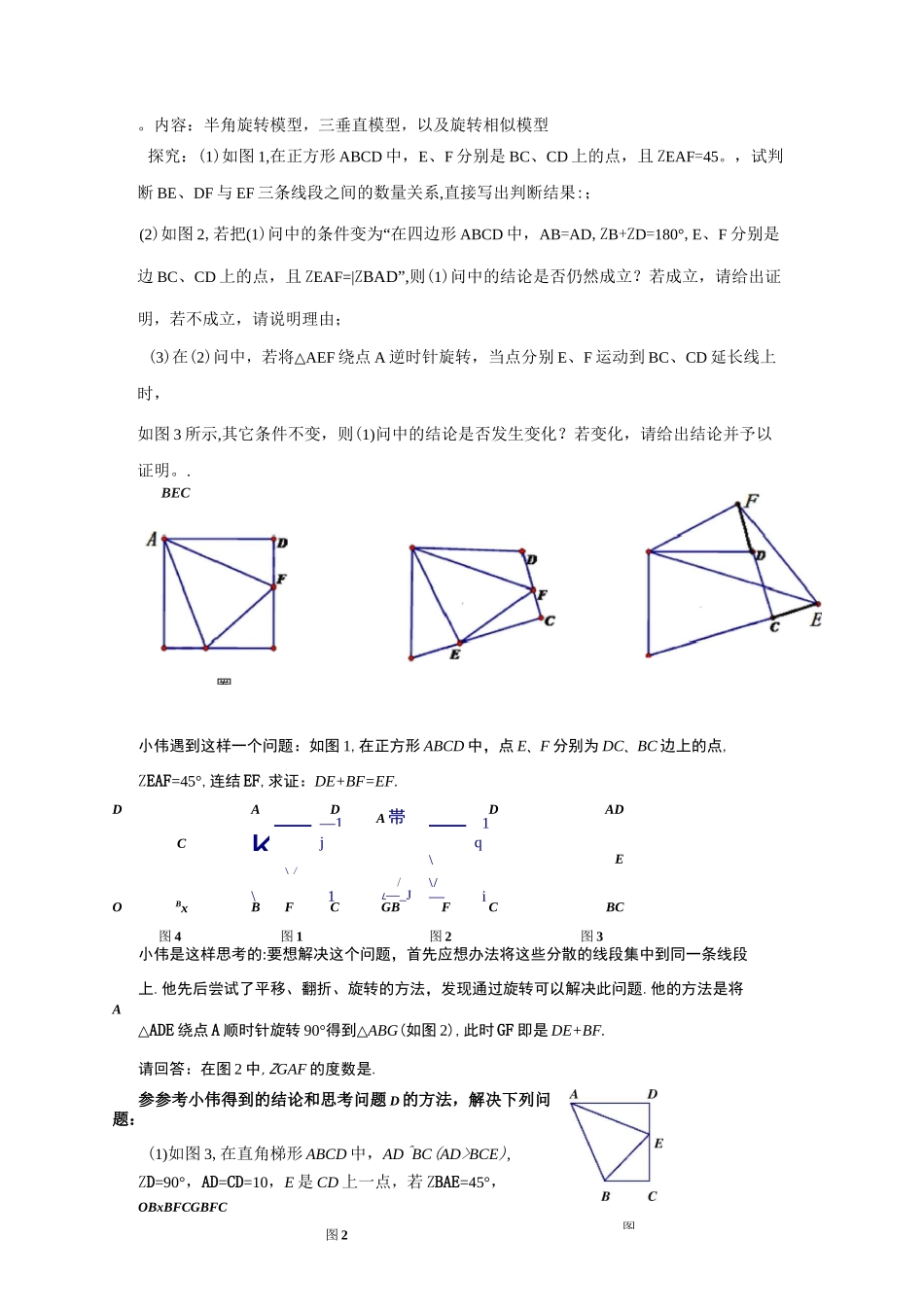
。内容:半角旋转模型,三垂直模型,以及旋转相似模型探究:(1)如图 1,在正方形 ABCD 中,E、F 分别是 BC、CD 上的点,且 ZEAF=45。,试判断 BE、DF 与 EF 三条线段之间的数量关系,直接写出判断结果:;(2)如图 2,若把(1)问中的条件变为“在四边形 ABCD 中,AB=AD,ZB+ZD=180°,E、F 分别是边 BC、CD 上的点,且 ZEAF=|ZBAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;(3)在(2)问中,若将△AEF 绕点 A 逆时针旋转,当点分别 E、F 运动到 BC、CD 延长线上时,如图 3 所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明。.小伟遇到这样一个问题:如图 1,在正方形 ABCD 中,点 E、F 分别为 DC、BC 边上的点,ZEAF=45°,连结 EF,求证:DE+BF=EF.DA —D—1A 帯 —D_1ADCKjq\E\//\/\__1L—_J—__iOBxBFCGBFCBC图 4图 1图 2图 3小伟是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.他的方法是将△ADE 绕点 A 顺时针旋转 90°得到△ABG(如图 2),此时 GF 即是 DE+BF.请回答:在图 2 中,ZGAF 的度数是.参参考小伟得到的结论和思考问题 D 的方法,解决下列问题:(1)如图 3,在直角梯形 ABCD 中,AD^BC(AD>BCE),ZD=90°,AD=CD=10,E 是 CD 上一点,若 ZBAE=45°,OBxBFCGBFC图 2BEC圏图ADE=4,贝 yBE=.(2)如图 4,在平面直角坐标系 xOy 中,点 B 是 x 轴上一动点,且点 A(-3,2),连结 AB 和 AO,并以 AB 为边向上作正方形 ABCD,若C(x,y),试用含 x 的代数式表示 y,贝卩 y=•已知:正方形 ABCD 中,AMAN=45,绕点 A 顺时针旋转,它的两边分别交 CB、DC(或它们的延长线)于点 M、N.(1) 如图 1,当 ZMAN 绕点 A 旋转到 BM 二 DN 时,有 BM+DN 二 MN.当 ZMAN绕点 A 旋转到 BM 丰 DN 时,如图 2,请问图 1 中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2) 当 ZMAN 绕点 A 旋转到如图 3 的位置时,线段 BM,DN 和 MN 之间有怎样的等量关系?请写出你的猜想,并证明.24.如图 1,在等腰直角△ABC 中,ZBAC=90°,AB=AC=2,点 E 是 BC 边上一点,ZDEF=45°且角的两边分别与边 AB,射线 CA 交于点 PQ(1)如图 2,若点 E 为 BC 中点,将 ZDEF ...