【数学】113导数的几何意义课件（人教A版选修2-2）VIP免费

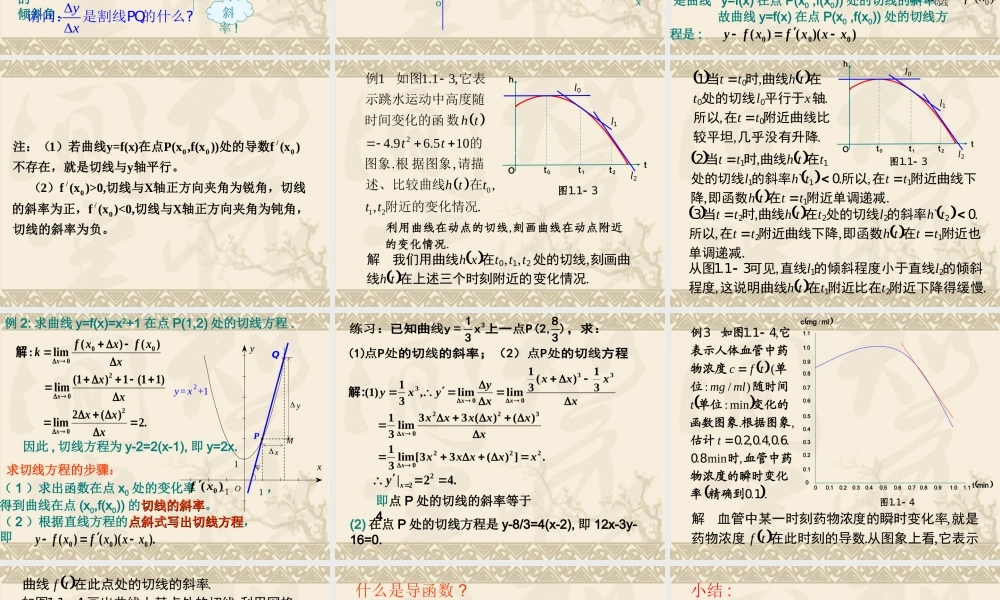
第一章 导数及其应用1.1.3 导数的几何意义 定义：函数 y=f(x) 在 x=x0 处的瞬时变化率是0000()()li.mlimxxf xxf xyxx   ,|)(00xxyxf或00000()()()limlim.xxf xxf xyfxxx  即：我们称它为函数 y=f(x) 在 x=x0 处的导数 , 记作 :回顾 由导数的意义可知 , 求函数 y=f(x) 在点 x0处的导数的基本方法是 :00(1)()();yf xxf x  求函数的增量00()()(2);f xxf xyxx 求平均变化率00(3)()lim.xyfxx 取极限，得导数 )2('),1('),(',)(12ffxfxxf求：设例的值代入求得导数值。再将自变量义求思路：先根据导数的定),(' xfxxxxxxxxxxxfxxfxfxxx2)2(lim)(lim)()(lim)('02200＝解：由导数的定义有422)(')2('2)1(2)(')1('21xxxffxff＝ 处的导数。在：求函数例12xxyxxxyxy1111解法一：21111lim0xx111xxxxxxxxxyxxxy1解法二：xxxxxyxx211limlim0021'1 xyxy21' 下面来看导数的几何意义 : βy=f(x)PQMΔxΔyOxyβPy=f(x) QMΔxΔyOxy 如图 , 曲线 C 是函数y=f(x)的图象 ,P(x0,y0) 是曲线 C 上的任意一点 ,Q(x0+Δx,y0+Δy)为 P 邻近一点 ,PQ 为 C 的割线 ,PM//x 轴 ,QM//y 轴 ,β 为 PQ的倾斜角 ..tan,,:xyyMQxMP则yx请问： 是割线PQ的什么?斜率 ! PQoxyy=f(x)割线切线T请看当点 Q 沿着曲线逐渐向点 P 接近时 , 割线 PQ 绕着点 P 逐渐转动的情况 . 我们发现 , 当点 Q 沿着曲线无限接近点 P 即Δx→0 时 , 割线 PQ 有一个确定位置 PT. 则我们把直线 PT 称为曲线在点 P 处的切线 . 设切线的倾斜角为 α, 那么当 Δx→0 时 , 割线 PQ 的斜率 , 称为曲线在点 P 处的切线的斜率 .即 :'00000()()()limlimxxf xxf xykf xxx  切线 这个概念 :① 提供了求曲线上某点切线的斜率的一种方法 ;② 切线斜率的本质——函数在 x=x0 处的导数 .导数的几何意义 函数 y=f(x) 在点 x0 处的导数的几何意义，就是曲线 y=f(x) 在点 P(x0 ,f(x0)) 处的切线的斜率 .即 :0'()kfx切线 故曲线 y=f(...