二次函数复习(数形结合)VIP免费

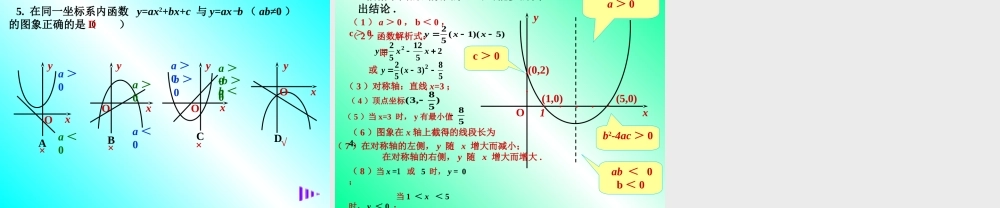
著名数学家华罗庚先生说：“数与形，本是相倚依，焉能分作两边飞；数无形时少直觉，形少数时难入微，数形结合百般好，隔离分家万事休，切莫忘，几何代数统一体，永远联系，切莫分离。” 数形结合 数形结合方法就是在解决和图形有关的问题时，将图形信息转换成代数信息，从而转化为代数问题；在解决与数量相关的问题时，根据数量的结构特征，构造出相应的图形，转化为几何问题，从而利用数形的辩证统一和各自的优势尽快地得到解题途径。 题型一、形帮数，让理性的数多一些感性。（ 1 ）右图是抛物线 的部分图像，从中你能得到哪些结论？)0(2acbxaxyo4xy-11 ），（ 01A（ 2 ）若直线与该抛物线交于 、两点，则你还可以从图中得到哪些结论？），（41B；的解为方程 2mkxcbxax；的解为不等式 2mkxcbxax；的解为不等式 2mkxcbxax根据右图，可以得到： （ 3 ）若双曲线 与该抛物线 交于 、 、 三点，你能否找出当 > 时相应的 x 的取值范围？xy13 )0(21acbxaxy），（313 A），（331B），（212C3y1yyxCBA 例 2 ：二次函数 的图象与 x 轴的两个交点 A 、 B 分别位于（－ 1 ， 0 ）点左侧，（ 1 ， 0 ）点右侧，试求 m 的取值范围。mxmxy2)2(2yxO1-1 题型二：数促形，让感性的形多一分理性例 3 ：（ 2011 广东肇庆）：已知抛物线 与 轴交于A （ ， 0 ）、 B （ ， 0 ）两点。若 (O 是坐标原点 ) ，求抛物线的解析式。)0(4322mmmxxy1x2x3211 OAOB 3 、“以数助形”“以形解数”例 5 ：如图，已知二次函数 的图象过点 C （ 0 ， ），与 x 轴交于两点 A 、 B ，且 求（ 1 ） A 、 B 两点的坐标； （ 2 ）求二次函数的解析式和顶点 P 的坐标； （ 3 ）若一次函数 y=kx+m 的图象的顶点 P ，把△ PAB 分成两个部分，其中一部分的面积不大于△ PAB 面积的，求 m 的取值范围。)0(2acbxaxy53OABPxMNYC12124,5xxx x 四：技能训练，有效提高 例 1 已知：如图是函数 y=ax2+bx+c （ a≠0) 的图象，试判断以下各式值的符号 （ 1 ） a ； （ 2 ） b ； （ 3 ） c ； （ 4 ） b2 － 4ac ；（ 5 ） a+b+c ；（ 6 ） a -b+c.解： 开口向下 ∴ a＜ 0 对称轴在 y 轴左侧 ∴ ab ＞ 0 ∴ b ＜ 0 与 y 轴...