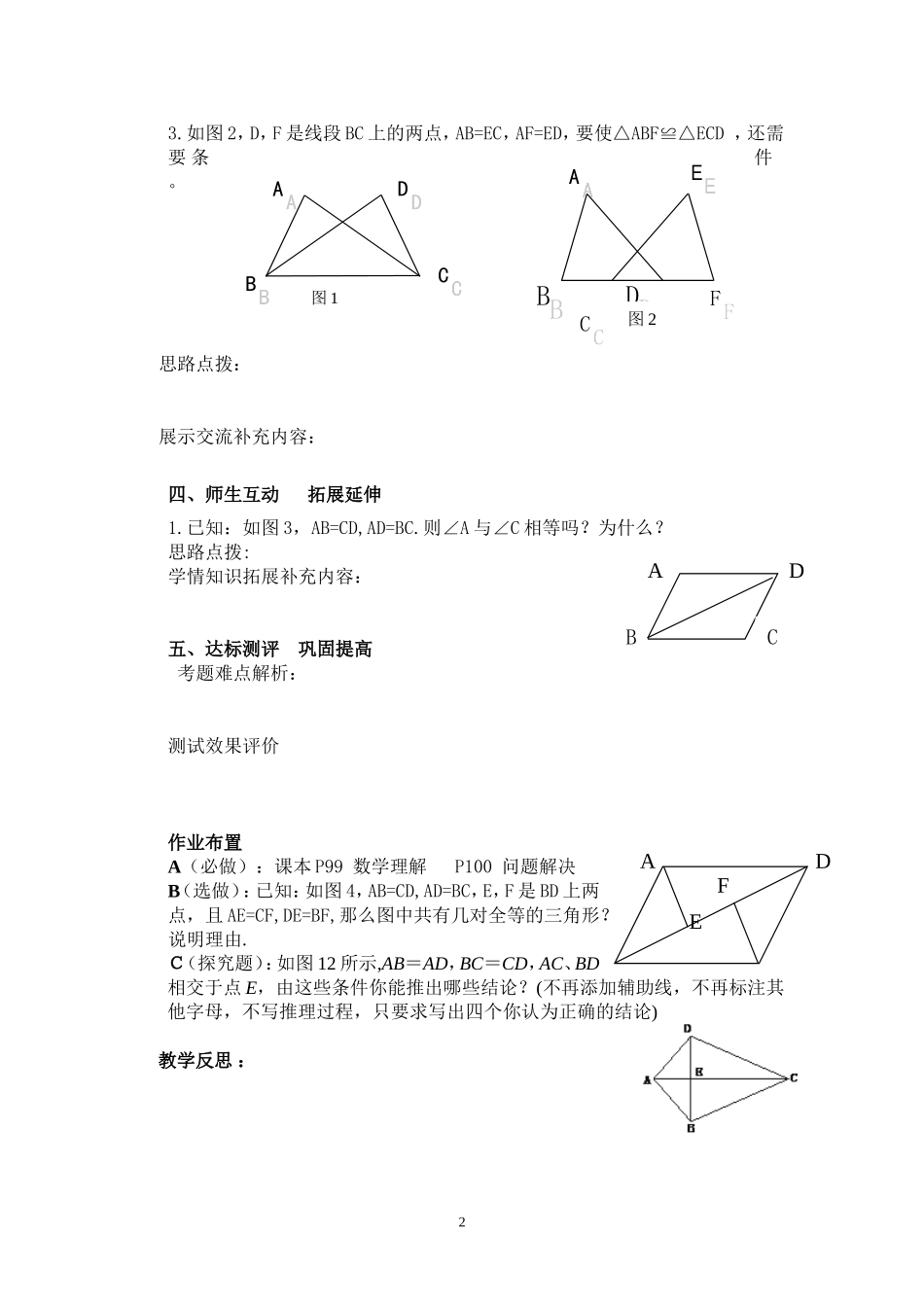
课时:5.3《探索三角形全等的条件 1》教学目标:1. 了解三角形的稳定性,三角形全等“边边边”的条件.2. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.3. 使学生在自主探索三角形全等的过程中,经历画图、观察、比较、交流等过程,从而获得正确的学习方式和良好的情感体验。4. 培养学生的空间观念,推理能力,发展有条理地表达能力,积累数学活动经验。重点:利用“边边边”的条件证明三角形全等。难点:探索三角形全等的条件.教学过程:一、预习反馈 明确目标:预习补充内容及疑点解析:二、创设情境 自主探究:1.探索三:给出三个条件画三角形时,有几种可能的情况?答:有 种。每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做 (1) 已知一个三角形的三个内角分别为 40°,60°和 80°。结论:三个内角对应相等的两个三角形 (填“一定”或“不一定”)全等。(2)已知一个三角形的三条边分别为 4cm,5cm 和 7cm。结论:三边对应相等的两个三角形 (填“一定”或“不一定”)全等,简写为 或 。 2.准备若干长度适中的小木条,用其中三根木条钉成一个三角形的框架,它的形状和大小是固定的吗?用四根小木条钉成的框架形状和大小固定吗?答:三角形的框架,它的大小和形状 (填“会”或“不会”)改变,四边形形的框架,它的大小和形状是 改变。3.三角形的稳定性:三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的 。思路点拨:探究问题补充内容:三、展示交流 点拨提升:“SSS”判定方法的应用1. 两个锐角对应相等的两个直角三角形全等吗?为什么?请画图说明。2.如图 1,AB=CD,AC=BD,△ABC 和△DCB 是否全等?试说明理由。 1如 图3B CB C如 图43.如图 2,D,F 是线段 BC 上的两点,AB=EC,AF=ED,要使△ABF≌△ECD ,还需要 条件 。 思路点拨:展示交流补充内容:四、师生互动 拓展延伸1.已知:如图 3,AB=CD,AD=BC.则∠A 与∠C 相等吗?为什么?思路点拨:学情知识拓展补充内容:五、达标测评 巩固提高考题难点解析:测试效果评价作业布置A(必做):课本 P99 数学理解 P100 问题解决B(选做):已知:如图 4,AB=CD,AD=BC,E,F 是 BD 上两点,且 AE=CF,DE=BF,那么图中共有几对全等的三角形?说明理由. C(探究题):如图 12 所示,AB=AD,BC=CD,AC、BD相交于点 E,由这些条件你能推出哪些结论?(不再添加辅助...